uBITXのスプリアス問題を改善したいという話の続き。
これまでの話はこちら。
LPF周りの改善案がいくつかあるが、ここでは、独自に設計してみる。
1.9 MHz(2.2MHz LPF)
uBITXでは本来は対応していない1.9MHz。使えれば儲けもの的にやってみる。
まずは、シミュレーション。いつものこちらのサイトを使わせてもらう。
以前の計算結果を踏まえ、カットオフ周波数2.2MHzで設計してみる。
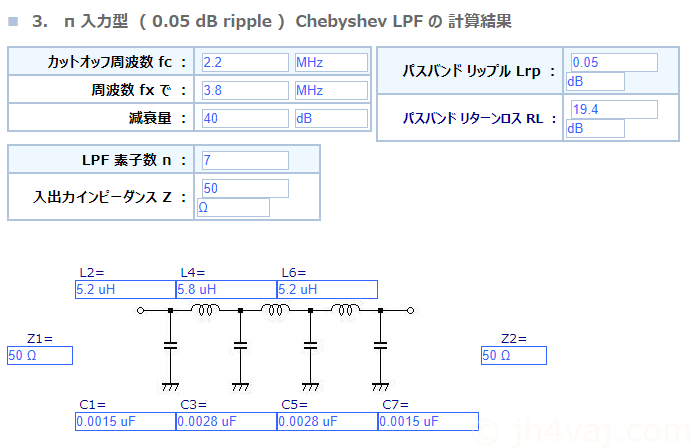
続いて、LTSpiceで特性を確認する。
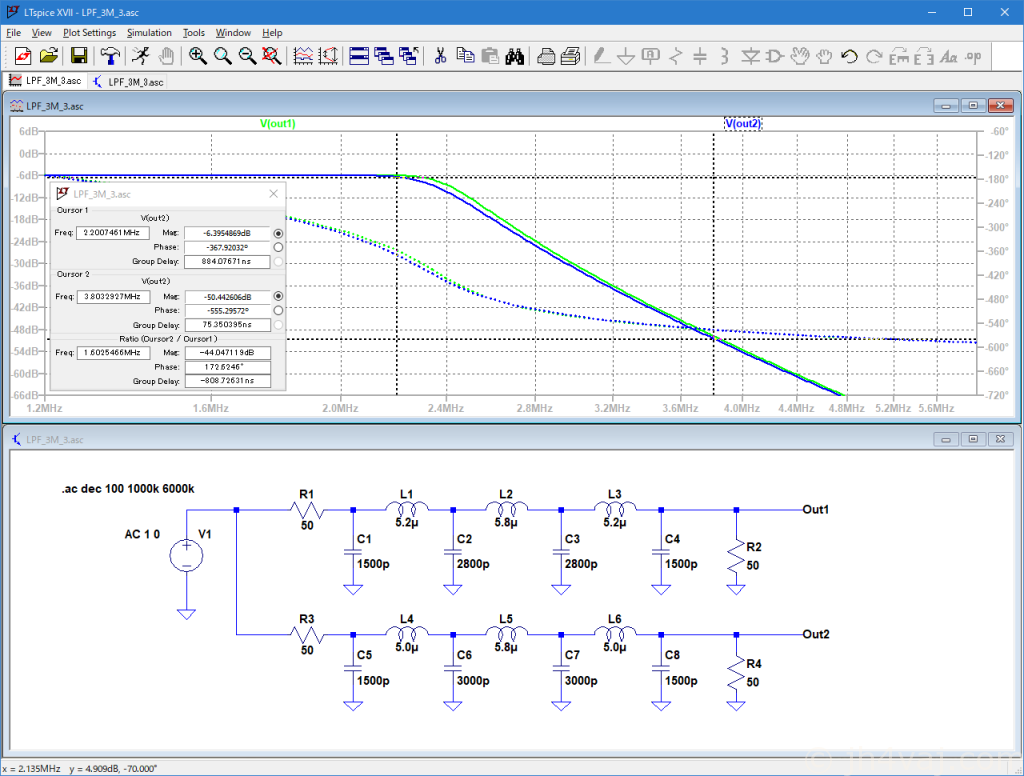
Out1(緑)が計算値。Out2(青)が実測したインダクタンス値と入手容易なキャパシタンス値。
では、実際に組んで測定。OSA103 Miniで周波数応答を見る。

基板は以前発注したもの。定数は後から変更できるので、大体のところで設計した。
コンデンサは50V耐圧の積層セラミック。なんだか心もとないけど、uBITXの基板に乗っているのは表面実装のチップコンデンサなので、ま、いいのかなと。ダメだったらそのときはそのとき。
そして、コイルは、こちらの記事で実測したもの。
では、測定結果。
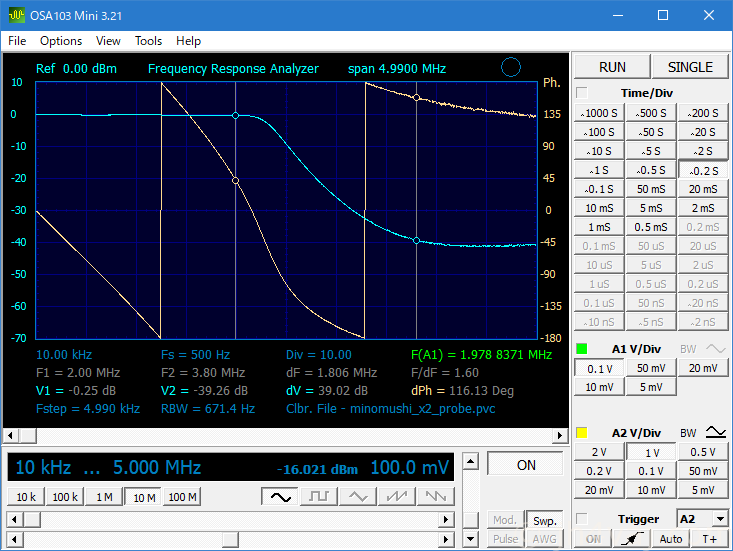
途中から減衰しなくなっているが、それを除いては、シミュレーション結果通り。
3.5 – 5 MHz(6MHz LPF)
近い将来、5MHz帯が開放されることを期待して、カットオフ周波数は6MHzで。しかし、そうすると、3.5MHzの第2次高調波の7MHzが近くなるため、フィルタを急峻にしなければなならない。そこで、リプルを0.1dBとやや緩めにして設計。
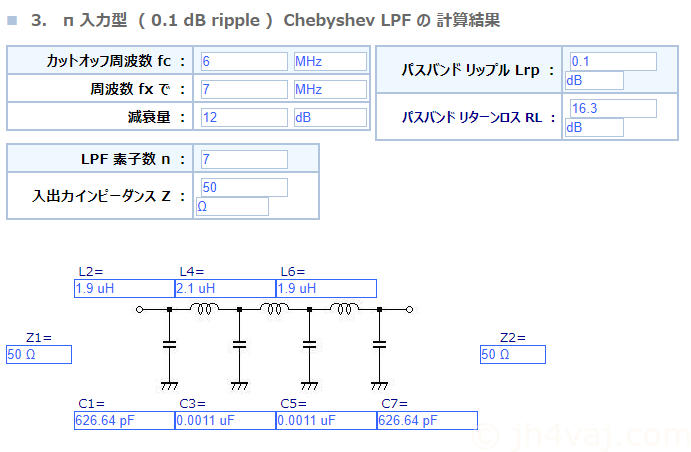
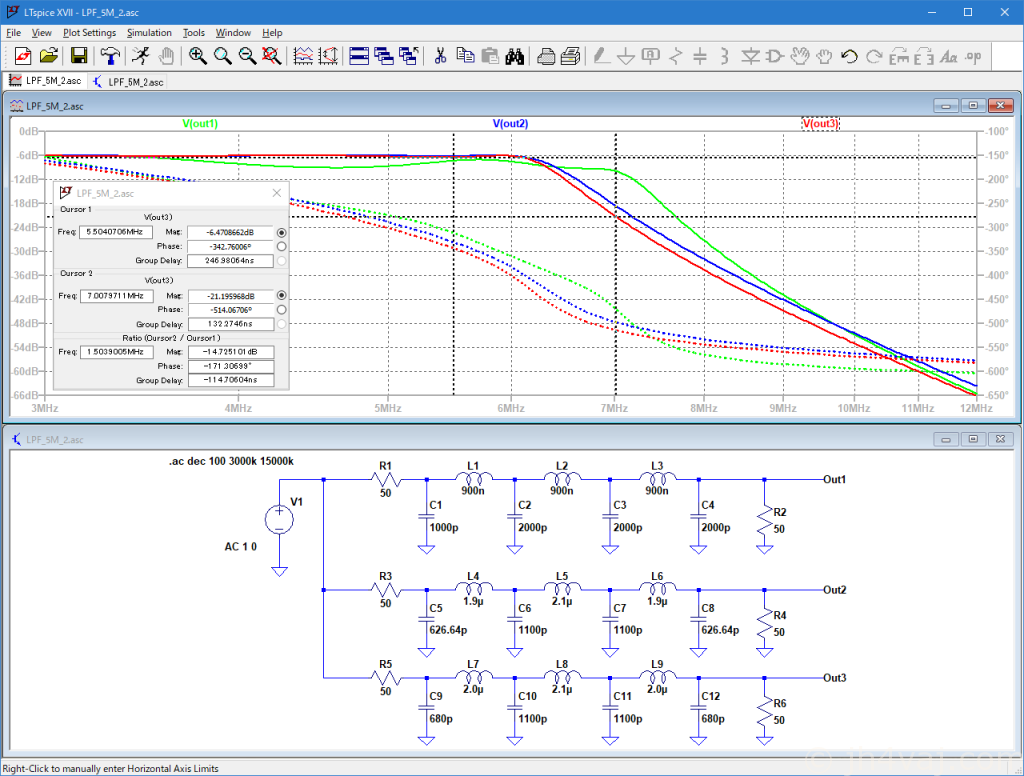
Out1(緑)はuBITXに元々搭載されているもの(回路図から読み取った定数)。Out2(青)が計算値。Out3(赤)が実測インダクタンス値と入手容易なキャパシタンス値。
3.5MHzの二倍の7MHzでの減衰量はこれで充分なのかどうなのか。全体を組んで測定してみてダメだったら5MHz対は諦めて、カットオフ周波数を下げて設計し直す。
実測。
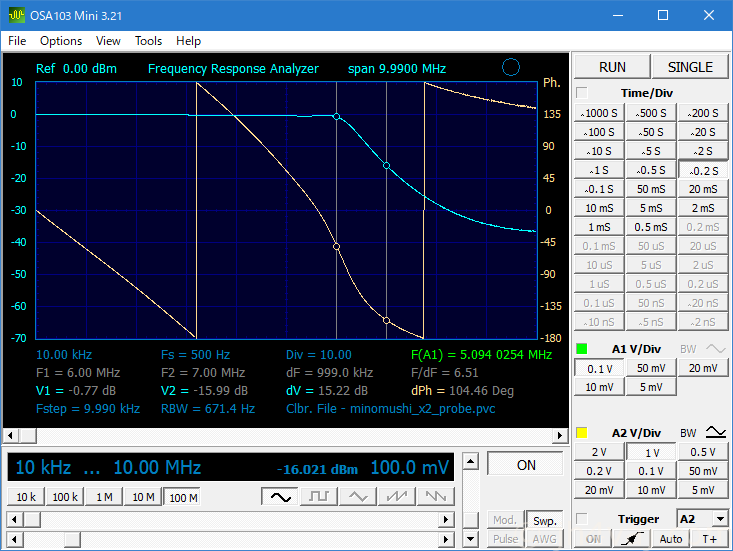
こちらも、途中から減衰しなくなっていることを除いて、シミュレーション結果通り。
7 – 10 MHz(10.8MHz LPF)
カットオフ周波数を10.8MHz、リプルを0.05dBと0.1dBの二つで計算。
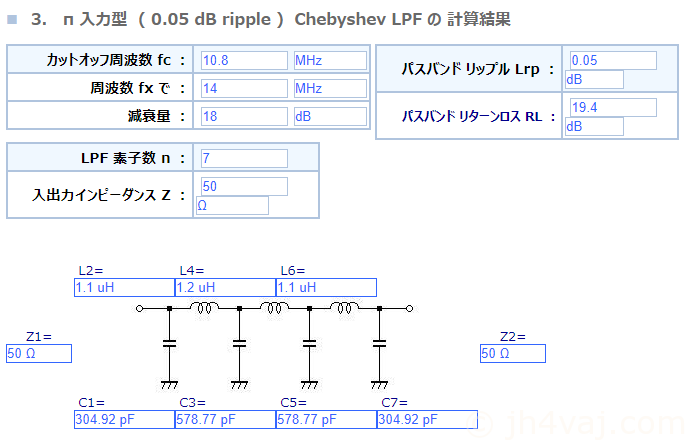
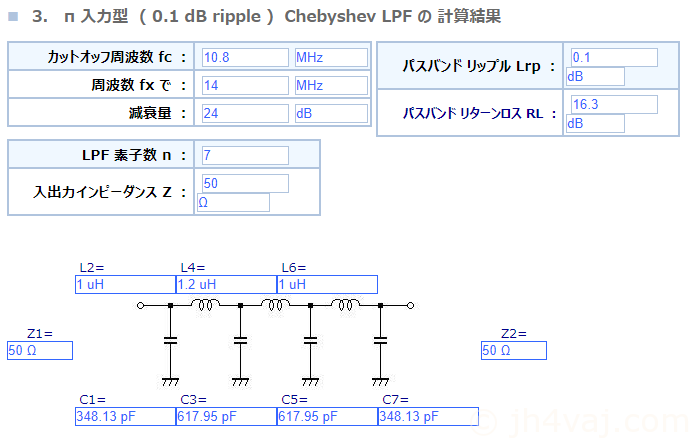
LTSpiceでシミュレーション。
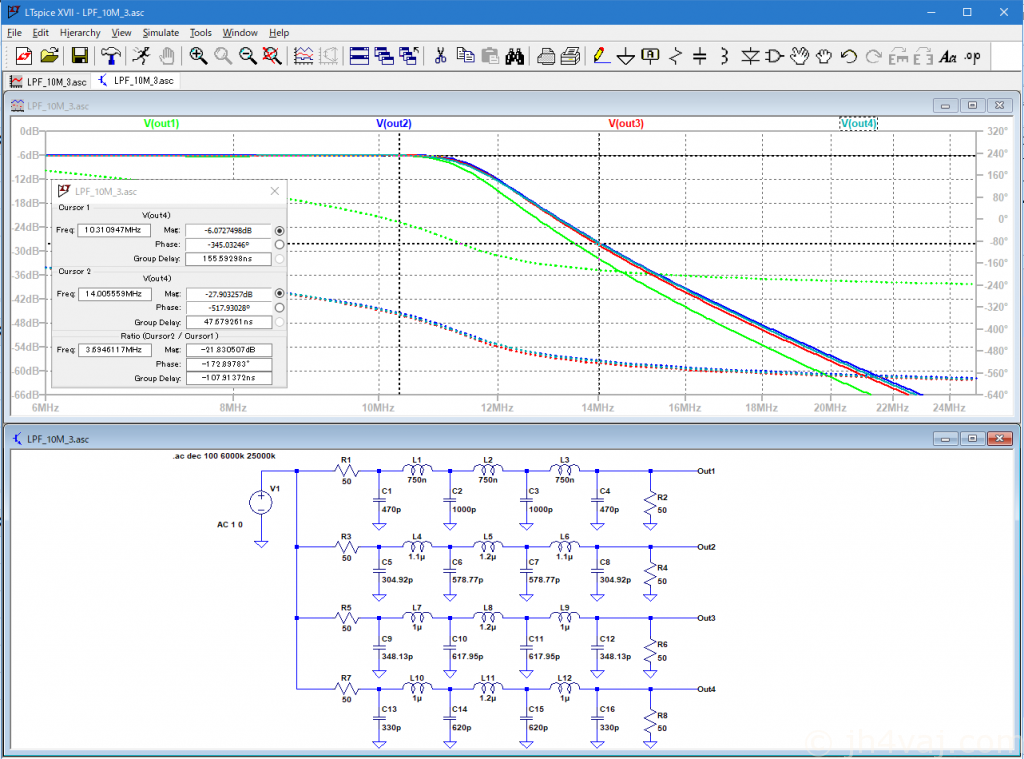
Out1(緑)はuBITXに元々搭載されているもの(回路図から読み取った定数)。Out2(青)がリプル0.05dBでの計算値。Out3(赤)がリプル0.1dBでの計算値。Out4(青緑かな?)が実測インダクタンス値と入手容易なキャパシタンス値。
なんと、元々のOut1が一番良さそう。しかし、よく見るとカットオフ周波数がちょっと低い。30mバンドの上限は10.150MHzなので、大丈夫かもしれないが。通過帯域付近を拡大して確認する。
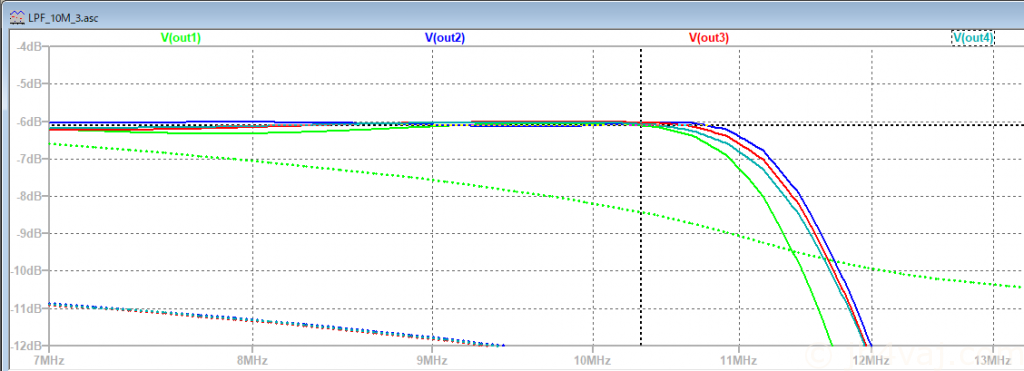
一応、バンド上限周波数も通りそうに見える。しかし、通過帯域のリプルが大きいことがわかる。
とりあえずは、設計値で組んで測定する。
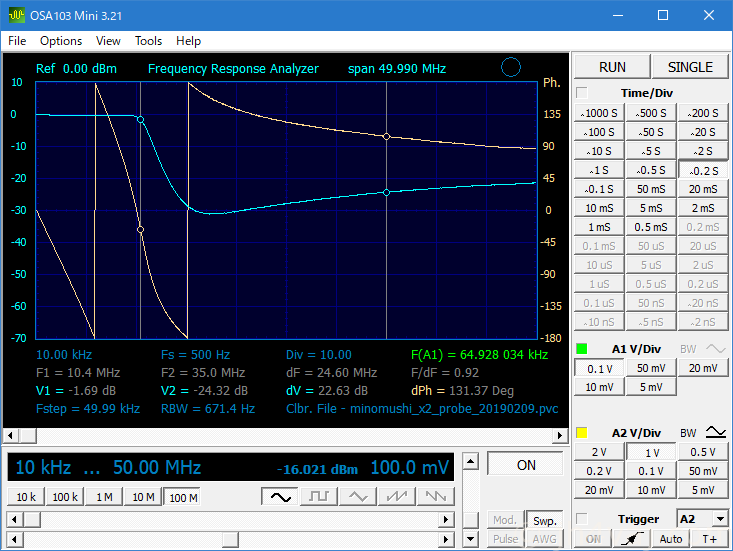
シミュレーションのカットオフ周波数よりも低いとこから落ち始めてしまっている。アマチュアバンドはぎりぎり通りそうだけど、微妙。
インダクタンス値をより実測値に近づけ、キャパシタンスを調整。
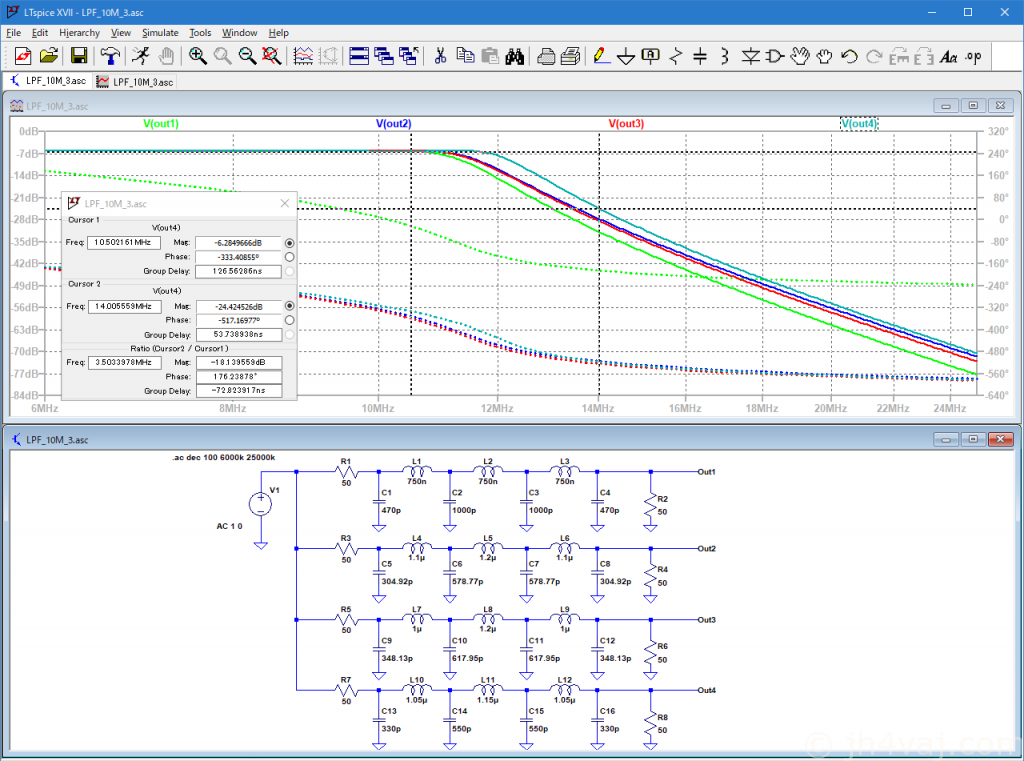
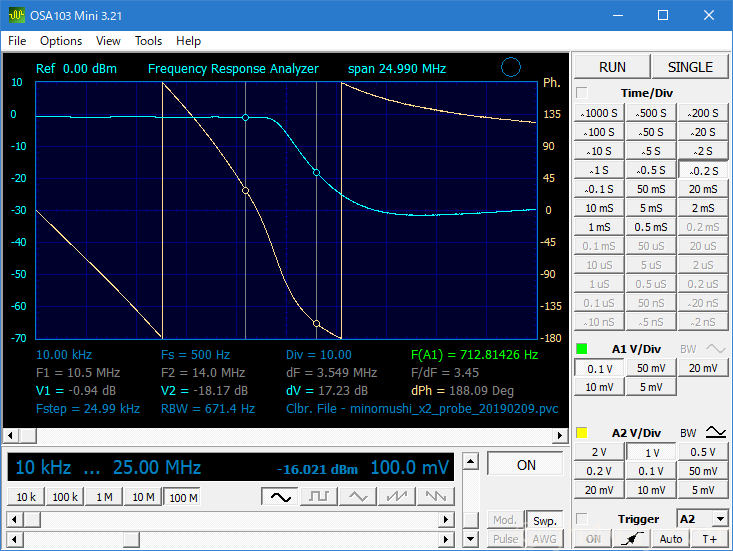
これならアマチュアバンドは余裕(上限は10.150MHz)。しかし、14MHz(7MHzの第2次高調波)でのフィルタの効きはちょっと甘い。ここは、最終的なスプリアスの状況を見て考える。
もう少し広いスパンでの測定結果。
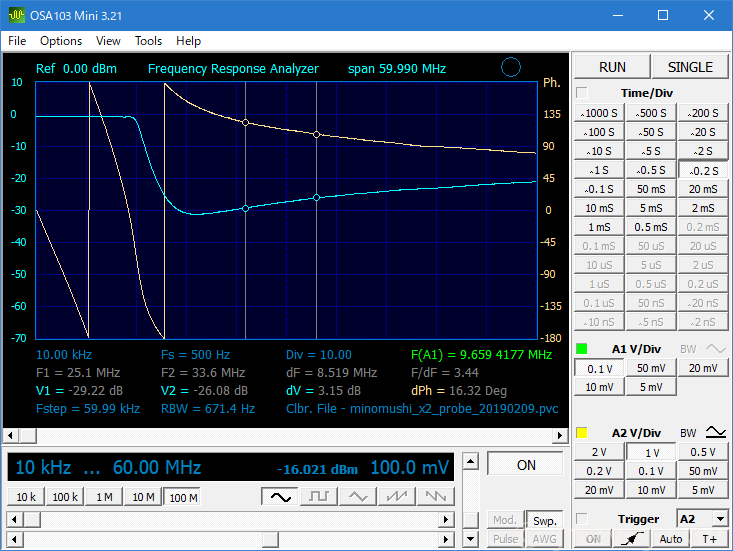
15MHz付近を底に、周波数が上がるとフィルタの効きが悪くなる。
14 – 21 MHz(22MHz LPF)
21MHz用のLPFはシビア。uBITXのIFは45MHzであるので、21MHzとの差分の23~24MHzが漏れ出る可能性がある。その対策の一例が下の記事。
これはこれとして、出力段でのLPFでもカットすることを考える。そうすると、通過帯域と遮断周波数が非常に近く、急峻な特性が求められる。ということで、フィルタの段数を増やして計算する。カットオフ周波数は22MHz、リプルは0.1dBで。
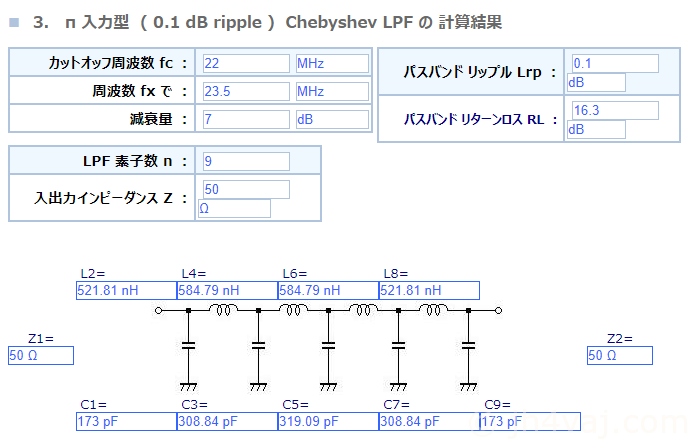
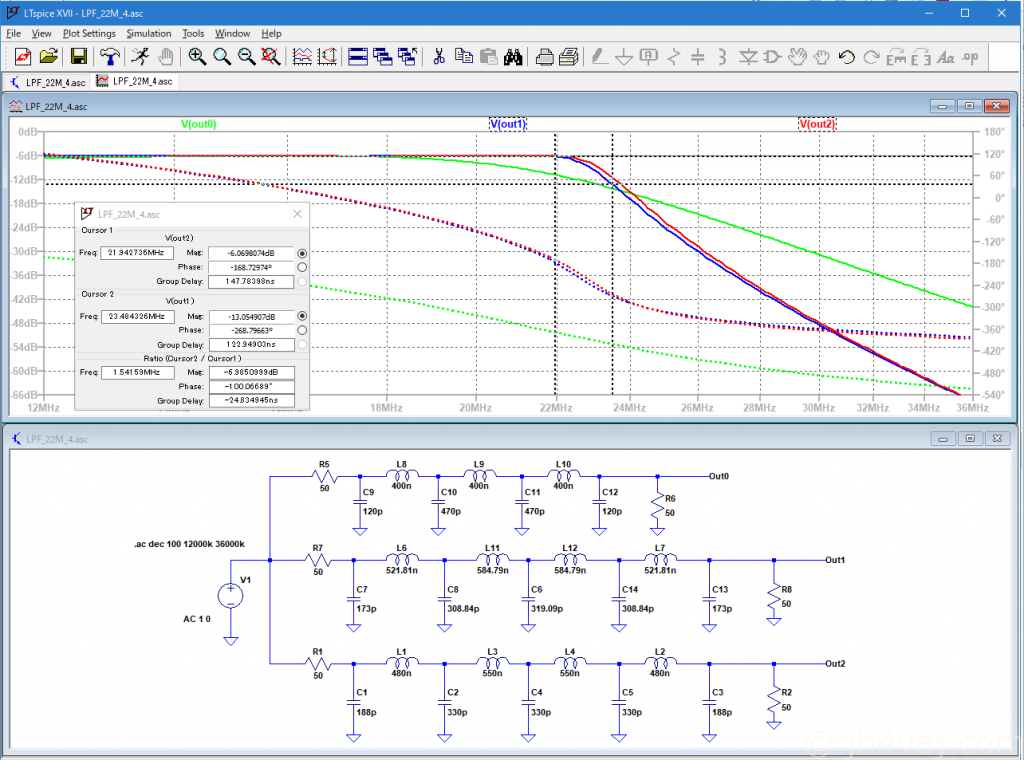
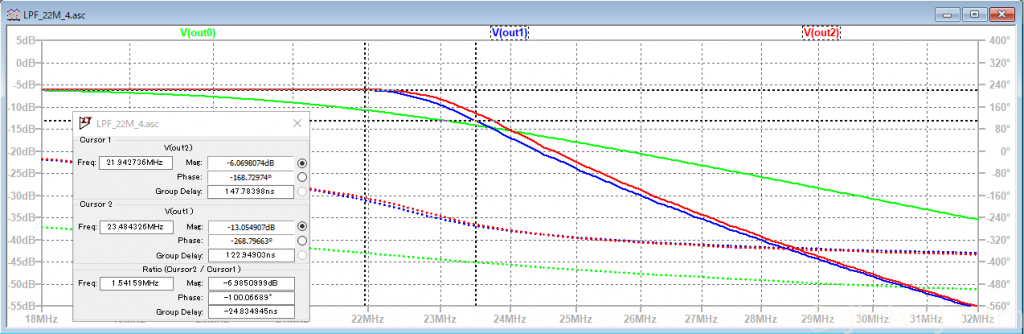
Out0(緑)はuBITXに元々搭載されているもの(回路図から読み取った定数)。Out1(青)が計算値。Out2(赤)が実測インダクタンス値と入手容易なキャパシタンス値。T37-6では計算値に近いインダクタンス値が得られず、やや離れた値。キャパシタンス値を調整して目的のカーブに近づけた。
しかし、実測結果は全然ダメ。
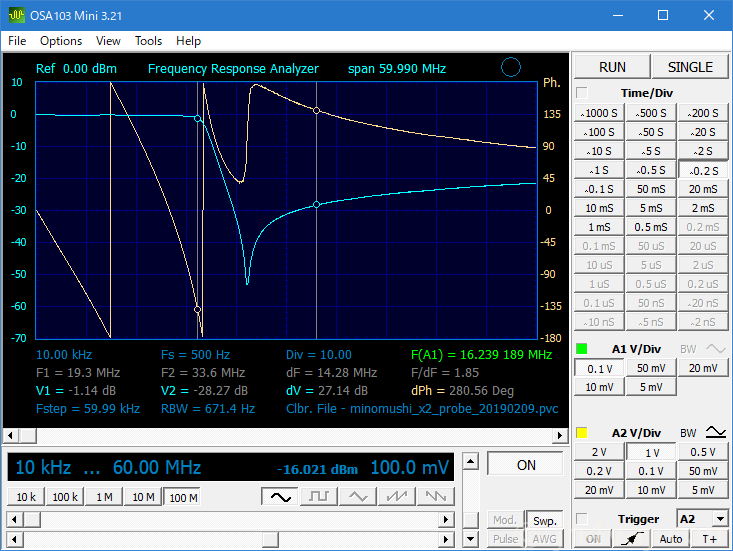
19MHzを超えたあたりから、すでに落ち始めている。
シミュレーションと実測を繰り返して、ここまで持ってきた。
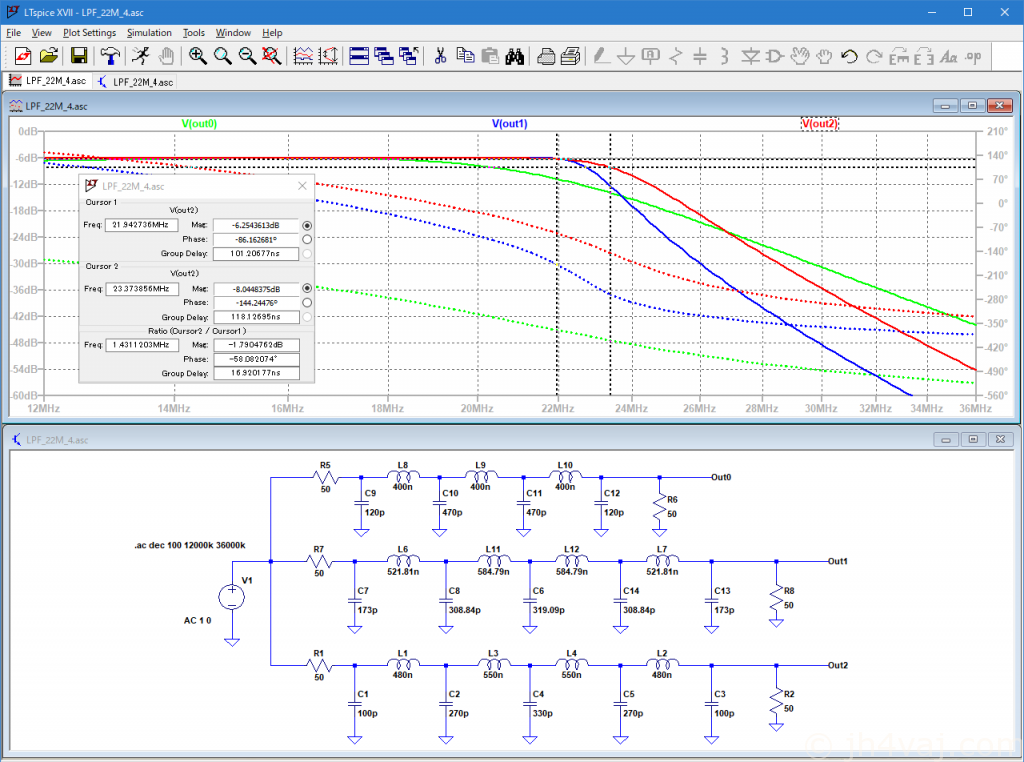
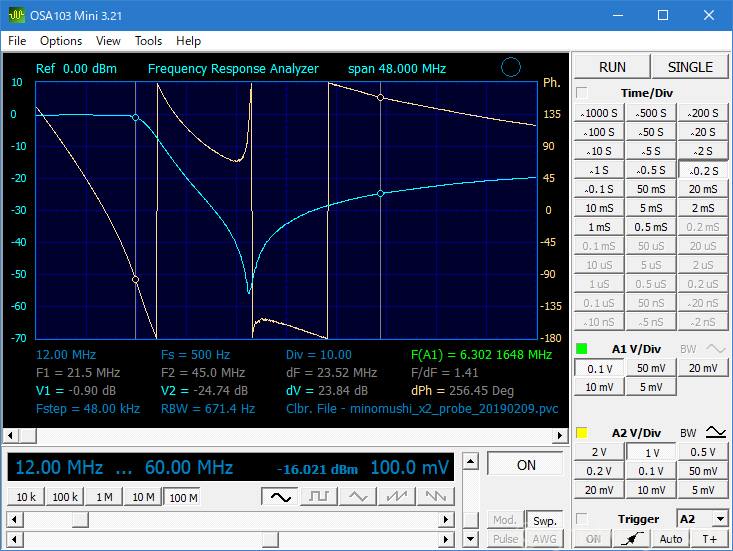
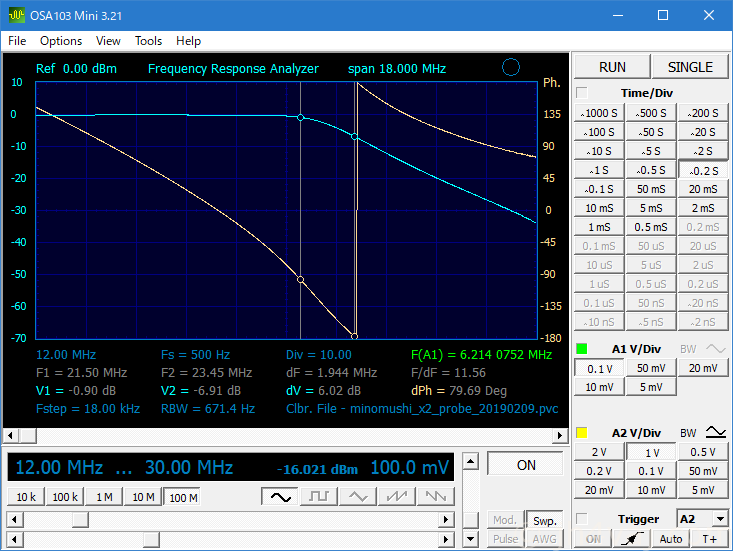
21MHz帯のバンドエッジ(21.450MHz)付近で少し落ち始めてしまっているが、仕方あるまい。もう少し上に広げることはできるが、そうすると落としたい23.5MHzあたりの効きが悪くなってしまう。これでもあまり効いているとは言えないし。まぁ、バンドの上限あたりで使うことはあまりないだろう。そもそも、「21.5MHzまでは通して、23.5MHzはしっかり落としたい」という仕様(希望)に無理があるわけで…。
でも、やっぱり悔しいので、もうちょっと頑張ってみた。
入力/出力側のコイルの巻数を一回増やしてみる(結果、すべて同じインダクタンス値に)。これでカットオフ周波数がちょっと上がる。しかも、カーブがやや急峻になるようだ(23.5MHz付近は甘くならない)。そして、キャパシタンス値をシミュレーションと実測で調整。最終結果がこちら。
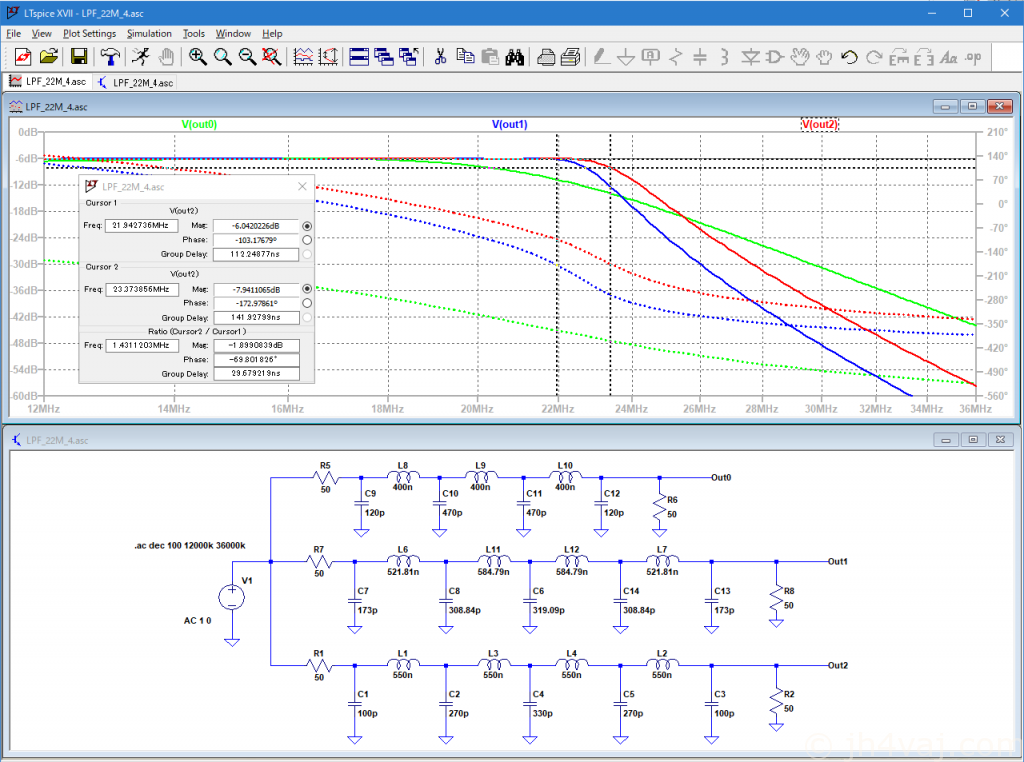
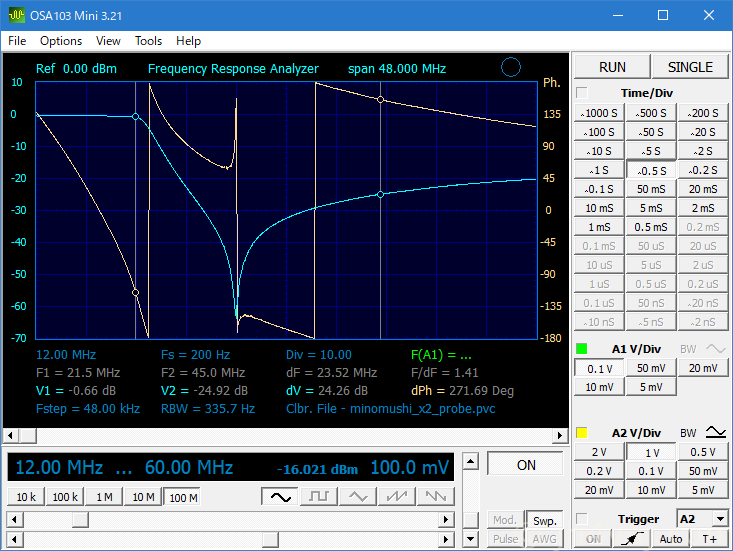
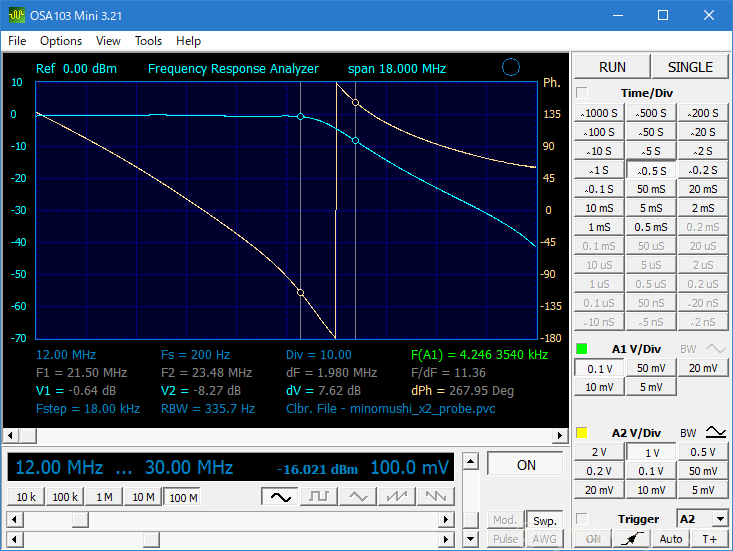
21.5MHz付近の減衰は若干少なくなり、23.5MHz付近の減衰は多少大きくなる。前のよりも改善しているので、これでよしとする。
24 – 28 MHz(27MHz BPF)
uBITXではこのバンド用のフィルタもLPFで構成されている。しかし、21MHz用で言及したように、IFとの差分の漏れが今度は下側に出てくる(45-24=21, 21<24)。そのため、BPFとして設計してみる。
バンドパスフィルタの設計
BPFの設計には、「LCフィルタの設計&製作」を参考にする。
大まかの流れは以下の通り。
- BPFの通過帯域分のLPFを作る。10~12MHzのBPFなら、2MHzのLPF。
- 幾何中心周波数\(f_0\)を求める。
- \(f_0\)を使って、LPFをBPF化する。
- イマジナリ・ジャイレータ変換で回路を整理する。
では、まず、通過周波数範囲の決定。少し余裕を見て、23.5~30.5MHzとする。したがって、通過帯域は7MHz。参考書に従い、まずは、7MHzのLPFを設計。BPFの場合はLCの数(素子数)が増えるためフィルタの段数を減らす。コイルを三つで構成することを念頭に、3次のフィルタとする。段数が減ると効果が下がるが、uBITXのそのままの測定結果を見るとハイバンドではスプリアスが非常に弱いので大丈夫だろうとの見込みで。
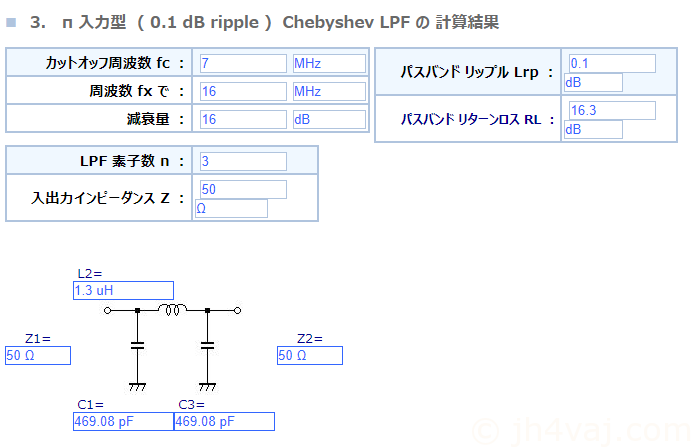
通過周波数範囲が23.5~30.5MHzなので、中心周波数は27MHz。また、通過帯域が7MHz。これらから、幾何中心周波数\(f_0\)を求める。
$$f_L=23.5\ MHz$$
$$f_H=30.5\ MHz$$
$$f_0=\sqrt{f_L \times f_H}=\sqrt{23.5 \times 30.5}=26.77\ MHz$$
$$\omega_0=2\pi f_0=2\pi \times 26.77\times 10^6$$
ここからBPF化する。CはLCの並列(書籍内では「I型」)に、LはLCの直列に(書籍内では「II型」)に変換する。
- I型(C→LC並列)の変換
\[
L_{1}=\frac{1}{{\omega_0}^2 \cdot C}\\
C_{1}=C
\]
- II型(L→LC直列)の変換
\[
C_{2}=\frac{1}{{\omega_0}^2 \cdot L}\\
L_{2}=L
\]
※ III型、IV型もあるが、ここでは割愛。詳細は、上記書籍で。
では、実際に変換する。
- C1=469.08 pF
\[
L_{1A}=\frac{1}{{\omega_0}^2 \cdot C1}\\
=\frac{1}{({2\pi \times 26.77\times 10^6})^2 \times 469.08 \times 10^{-12}}\\
=75.35\times 10^{-9}=75.35\ nH
\]
\[
C_{1A}=C1=469.08\ pF
\]
- C3=469.08 pF
C1と同じ。 -
L2=1.3µH
\[
C_{2B}=\frac{1}{{\omega_0}^2 \cdot L2}\\
=\frac{1}{({2\pi \times 26.77\times 10^6})^2 \times 1.3 \times 10^{-6}}\\
=27.19\times 10^{-12}=27.19\ pF
\]
\[
L_{2B}=L2=1.3\ \mu H
\]
この後、イマジナリ・ジャイレータ変換によって、LCの並列をLCの直列に(またはその逆に)変換して回路を整理する。ここで気づいた。それだったら、π型よりもT型で組んだ方が楽じゃないかと。いや、本当は、フィルタの段数や帯域などいろいろ試行錯誤したのだけど、そこまで触れるとうるさくなりすぎるので、それは省略。
T型ベースに変更
では、改めて、T型で。帯域や幾何中心周波数(\(f_0\))は上と同じ。
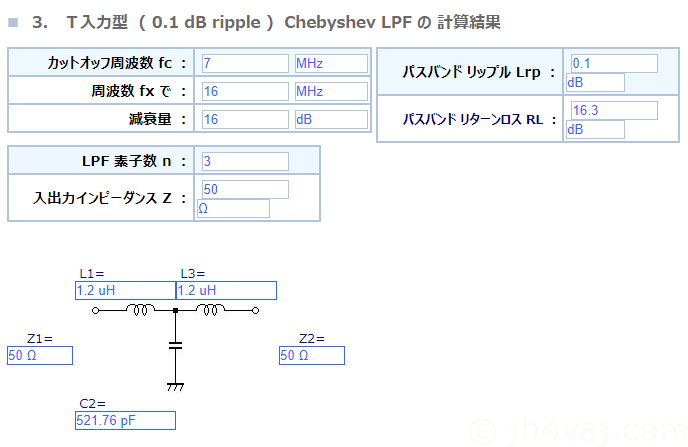
L、Cを変換して、BPF化する。この手順も同じ。
- L1=1.2µH
\[
C_{1B}=\frac{1}{{\omega_0}^2 \cdot L2}\\
=\frac{1}{({2\pi \times 26.77\times 10^6})^2 \times 1.2 \times 10^{-6}}\\
=29.46\times 10^{-12}=29.46\ pF
\]
\[
L_{1B}=L1=1.2\ \mu H
\]
- L3=1.2µH
L1と同じ。 -
C2=521.76 pF
\[
L_{2A}=\frac{1}{{\omega_0}^2 \cdot C1}\\
=\frac{1}{({2\pi \times 26.77\times 10^6})^2 \times 469.08 \times 10^{-12}}\\
=67.74\times 10^{-9}=67.74\ nH
\]
\[
C_{2A}=C2=521.76\ pF
\]
とりあえず、ここまででLTSpiceでシミュレート。
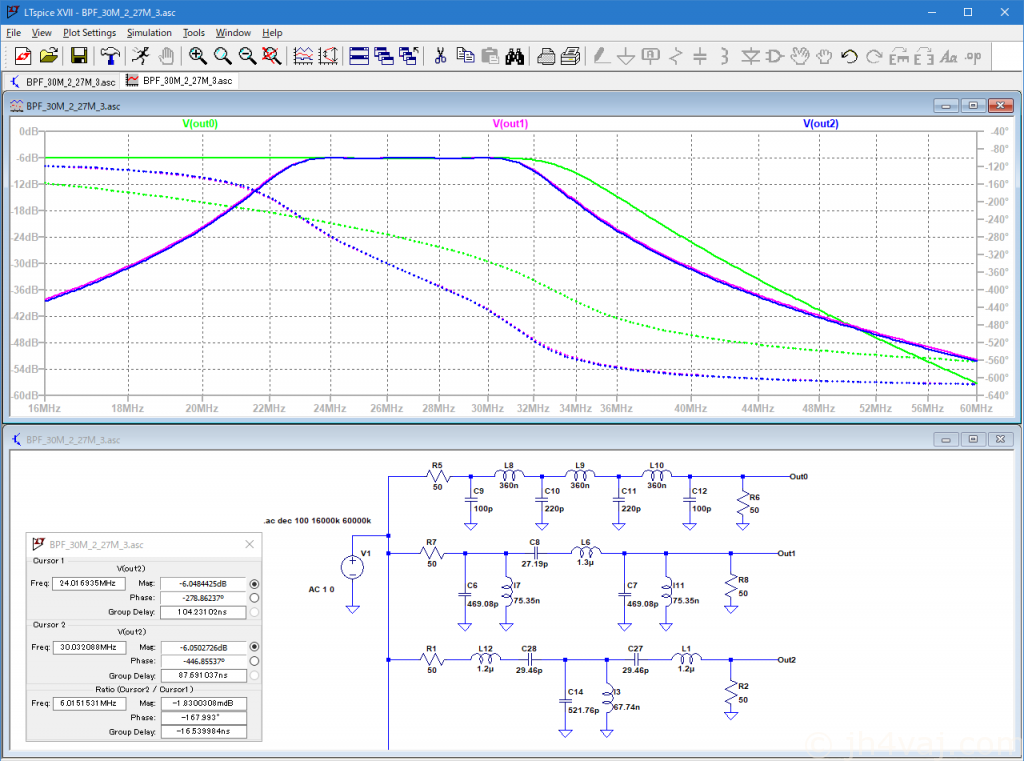
Out0(緑)はuBITXに元々搭載されているもの(回路図から読み取った定数)。Out1(ピンク)がπ型LPFを元にしたBPF。Out2(青)がT型LPFを元にしたBPF。π型、T型、どちらをベースにしてもほぼ同じ特性が得られることがわかる。
イマジナリ・ジャイレータ変換
イマジナリ・ジャイレータ変換を行う。ここでの変換対象は、L2AとC2Aの並列部。最初の条件は、L2AをL1BやL3Bと同じ値にすること。
\[
L_{2A2} \times C_{2A2} = L_{2A} \times C_{2A}\\
C_{2A2} = \frac{L_{2A} \times C_{2A}}{L_{2A2}}\\
= \frac{67.74\ nH \times 521.76\ pF}{1.2\ \mu H}\\
=29.54\ pF
\]
\[
C=\frac{1}{\omega_0}\sqrt{\frac{C_{2A2}}{L_{2A}}}\\
=\frac{1}{2\pi \times 26.77\times 10^6}\sqrt{\frac{29.54\times 10^{-12}}{67.74\times 10^{-9}}}\\
= 124.15\times 10^{-12} = 124.15\ pF
\]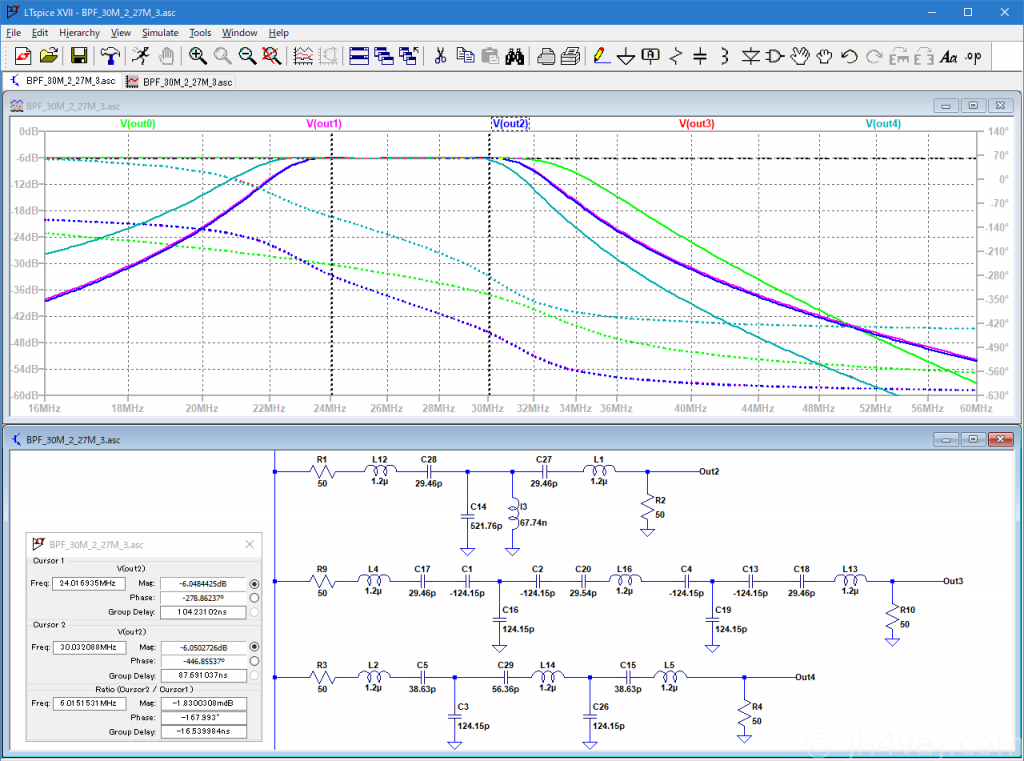
Out3(赤)がジャイレータ変換を行ったもの。Out4(青緑)がはコンデンサを整理したもの。両者はピッタリ重なっているので一本しか見えない。ジャイレータ変換では、元とは完全には同じならないことが参考書にも書かれていた。なので、こんなものか。とはいえ、通過帯域が下にずれてしまっているので、なんとかしたい。それにしても、LTSpiceってマイナスのキャパシタンス値でもちゃんとシミュレートしてくれるんだ。すごい。
続いて、現実の定数でのシミュレート。Out5(灰)がそのグラフ。
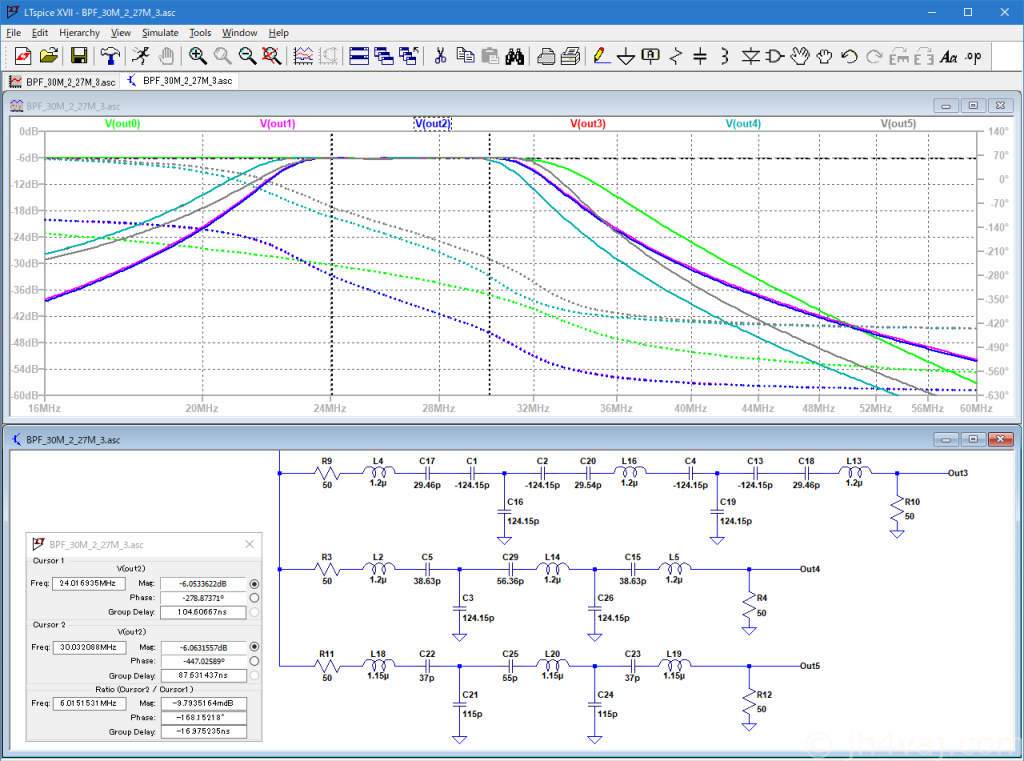
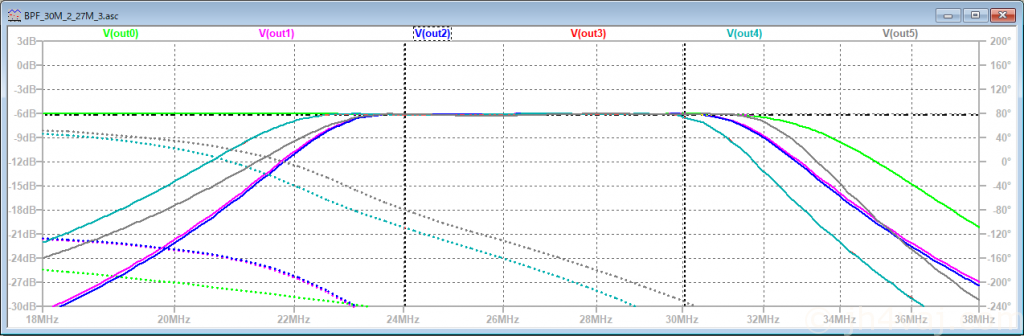
もう少し定数を調整(C21, C24を115pF→122pF)。
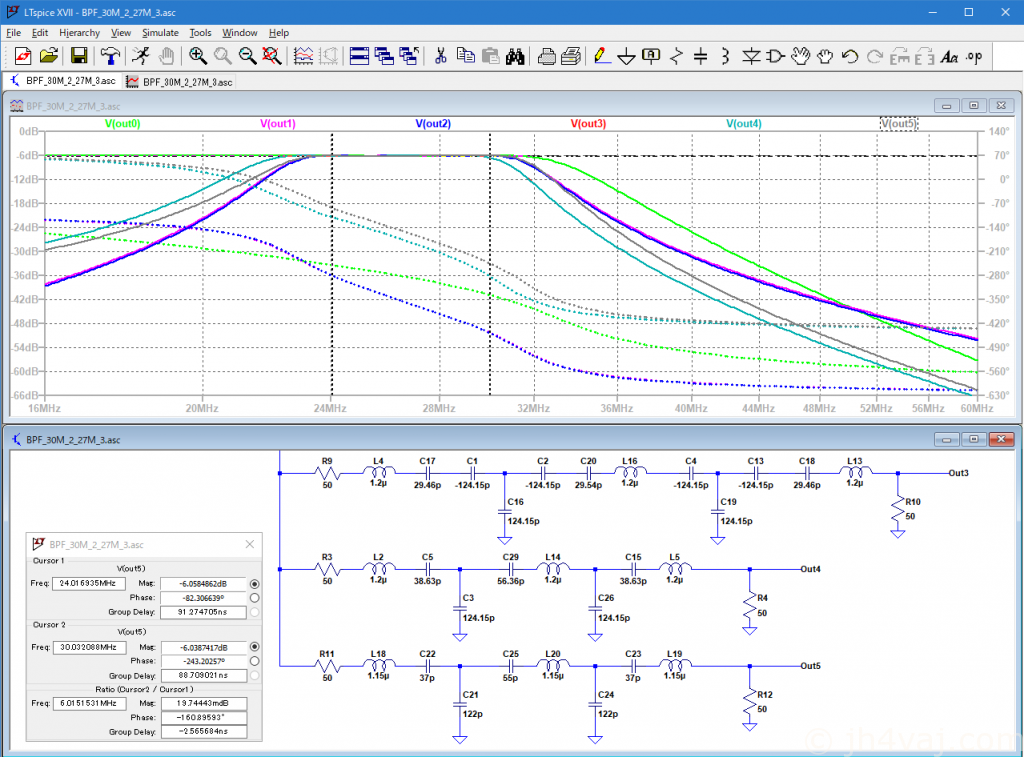
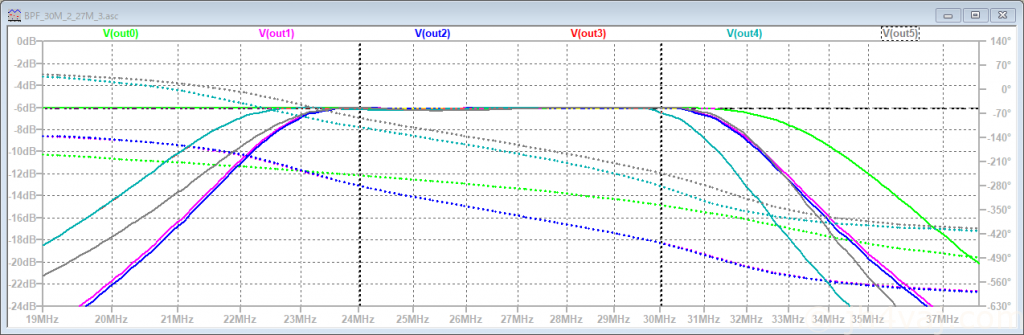
いろいろいじったが、この辺が限界。これは実現できるんだろうか?しかし、これだったら、ジャイレータ変換しないで検討した方がいいかも。とはいえ、すでに基板は作ってあるので仕方ない。下は甘くなっているけど、上は厳しくなっているわけで、ま、いいか。
では、実測。なお、15pFの手持ちが残念ながらなかったので、37pF(15+22pF)は諦めて、33pFで組んだ。
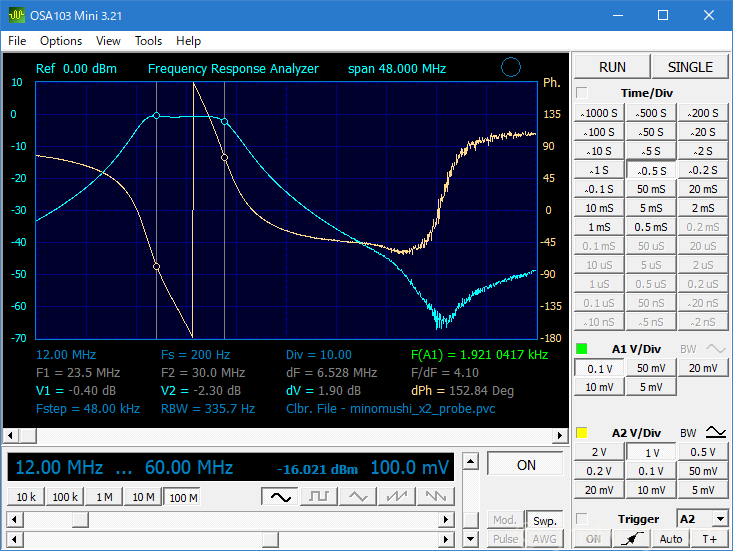
うーん、通過帯域が下にずれている。
キャパシタンス値をいじって、帯域を上にずらしてみる。
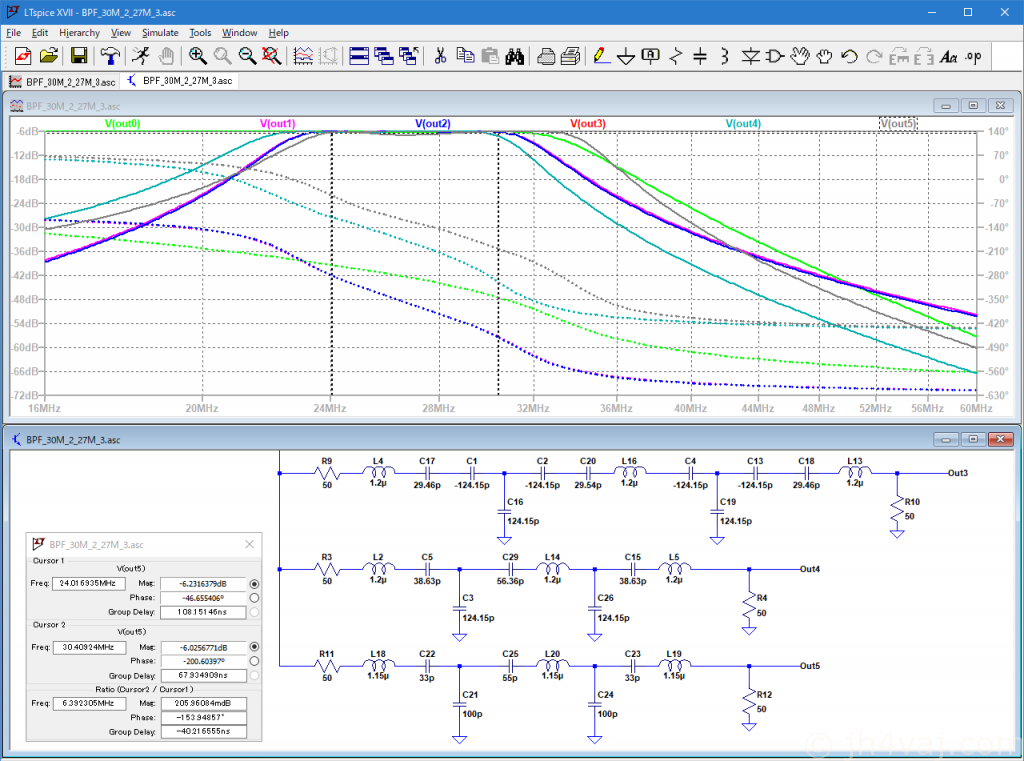
実測。
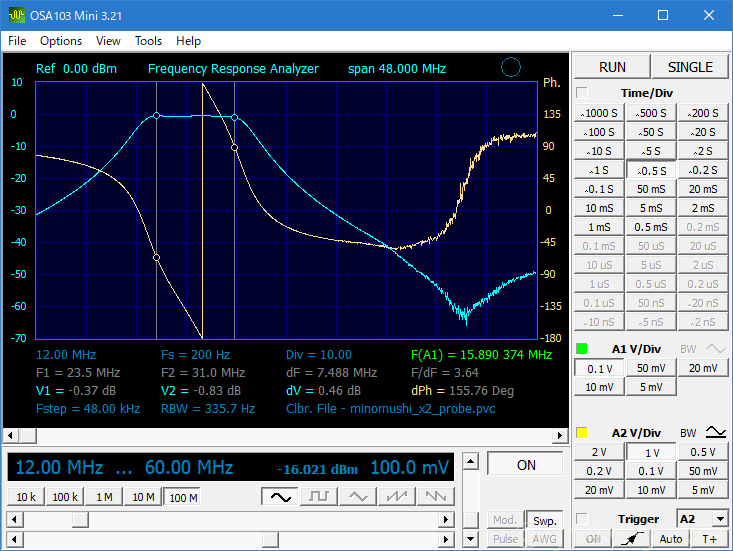
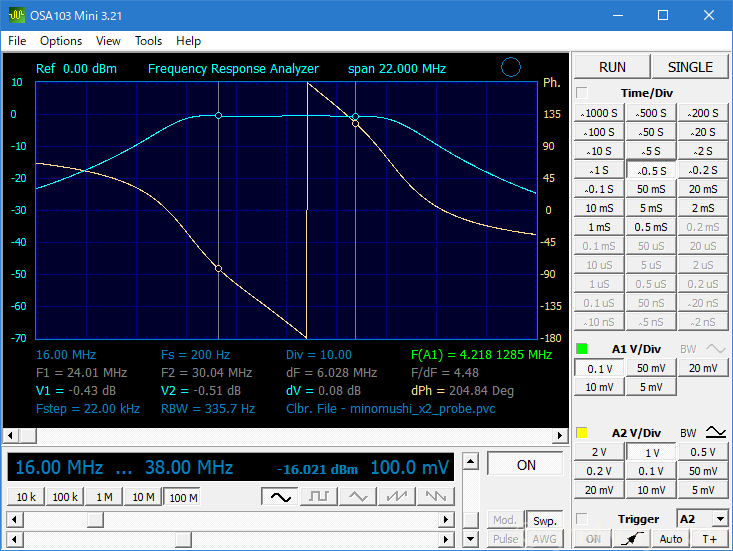
まぁ、割といいかな?下をもっときつくしたい気がしないでもない。10pF足す?とりあえずはこのままにしておこう。
それにしても、段数を減らしたので、全体的に切れが甘い。基板を作り直したい衝動に駆られる…。ま、それは全部組んで、その結果を見てから。作り直さなくて済みますように。
まとめなど
周波数が高くなるに連れ、シミュレーション通りにならないのは、分布容量や浮遊容量の影響か?
途中、「コンデンサは交換するから」と、横着して足を切らずに基盤につけて測定していた。「シミュレーション値とずいぶん合わないなぁ」と思いながら追い込んで、最後に足を切って付けたらぜんぜん違う特性になってしまった。わずか数cmとはいえ、大きく影響していることが実感できた。やはり、「配線は最短長で」だな。
下の写真は周辺回路も載せた状態。最終的には、コイルはホットボンドで固定した方がいいかも。







コメント