「アンテナのSWRを測るときはアンテナ直下で」とよく言われる。もしくは、「同軸ケーブルの長さは(電気的)λ/2で」と。そのあたりの話はこちらの参考サイトで。
もう一つ、こちらも。
この話はこの話として、それ以外にも同軸ケーブルの損失によってSWRが良く見えてしまう。
SWRの計算式
通過型のSWR計の場合、進行波電力と反射波電力からSWR(VSWR)を求めている。
$$VSWR = \frac{1+\sqrt{\frac{P_r}{P_f}}}{1-\sqrt{\frac{P_r}{P_f}}}$$
ここで、Pf: 進行波電力、Pr: 反射波電力。
まったく反射しない場合を考えてみる。仮に、進行波電力を10W、反射波電力が0Wとするとこうなる。
$$VSWR = \frac{1+\sqrt{\frac{0}{10}}}{1-\sqrt{\frac{0}{10}}} = \frac{1+0}{1-0} = 1$$
これは整合が取れている状態。
逆にすべて反射すると、進行波電力が10W、反射波電力も10W。
$$VSWR = \frac{1+\sqrt{\frac{10}{10}}}{1-\sqrt{\frac{10}{10}}} = \frac{1+1}{1-1} = \frac{2}{0}$$
分母がゼロなので、VSWRは無限大。これは、短絡しているか開放の状態。
※計算するなら1Wの方が簡単だけど、10Wの方がなんとなく実感が湧くのでそうしてみた。
参考サイト:
同軸ケーブルの損失の影響
同軸ケーブルには損失があるため、仮に全反射したとしても、戻ってきた反射波電力は損失の分だけ小さくなってしまう。
仮に、10dBの損失なら、10Wを入力して同軸ケーブルの先端は-10dB(1/10)の1Wになり、それが全反射して手元に戻ってきたときにはさらに-10dBの0.1Wになる。先程の計算式に当てはめるとこうなる。
$$VSWR = \frac{1+\sqrt{\frac{0.1}{10}}}{1-\sqrt{\frac{0.1}{10}}} = \frac{1+\sqrt{0.01}}{1-\sqrt{0.01}} = \frac{1.1}{0.9} = 1.22$$
本来なら無限大なものが1.22に見えてしまうという結果。10dBの減衰があると、たとえアンテナが接続されていなくても「1.2位だからOK!」となってしまう。
実験
計算だけでは面白くないので、実際に測定してみる。
20dBアッテネータ
手元に20dB(1/100)のアッテネータがあるので、これを使う。まずは、計算。10Wを入れたとすると、反射波は0.01Wになる。
$$VSWR = \frac{1+\sqrt{\frac{0.01}{10}}}{1-\sqrt{\frac{0.01}{10}}} = \frac{1+\sqrt{0.001}}{1-\sqrt{0.001}} = 1.07$$
実測。オープン状態(アッテネータなし)。

19.99はこのSWR計の最大値。これ以上は表示できない。
では、20dBのアッテネータを接続。アッテネータの先はオープン。


1.09。計算値とだいたい一致。
同軸ケーブル
いつも使っている、RG-58C/U 10m。まずは、NanoVNAでロスを測る。その前に、NanoVNAにプローブ用の同時ケーブルを付けた状態を確認。
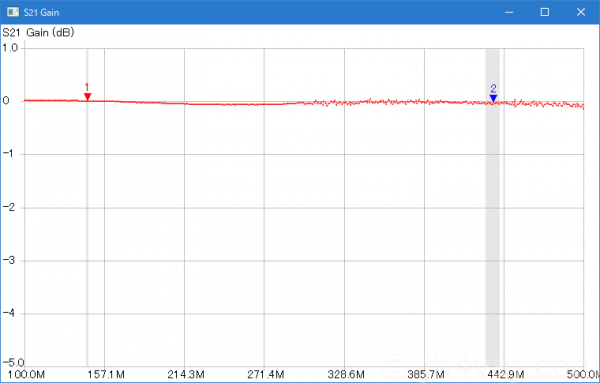
キャリブレーションを行う際に、CH0とCH1の両方にプローブ用の同軸ケーブルをつないでそれをSMAメス-メスコネクタでつないだもの。まぁ、これくらいならいいかな。
では、同軸ケーブルの通過特性。
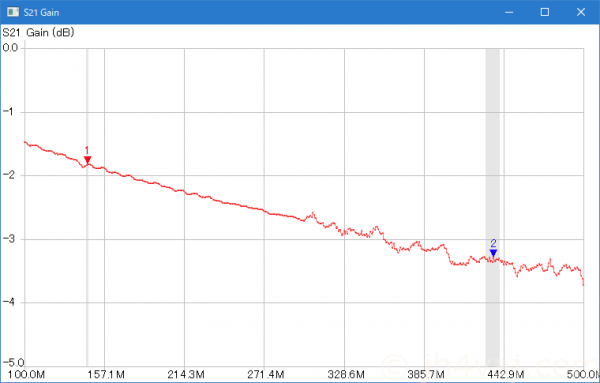
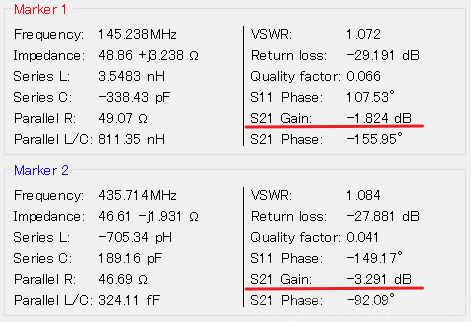
435MHzあたりで約-3.3dB。SMA-BNC変換を二つ通している点には注意(その分、減衰が多めに出ていると考えられる)。
これを元に計算してみる。反射波は同軸ケーブルの減衰の影響を往復で受けるので6.6dB。入力が10Wだとすると、反射波は2.19W。

$$VSWR = \frac{1+\sqrt{\frac{2.19}{10}}}{1-\sqrt{\frac{2.19}{10}}} = 2.76$$
実測。


計算値よりも「良い値」になった。
ともかく、同軸ケーブルによるロスによって見かけ上のSWRがよくなることは確認できた。
【追記】このSWR計は表示値がおかしい。
リターンロス
上のところまで書いて投稿したら、これはリターンロスのことだと教えていただいた。
なるほど。断片的な知識がつながった。ありがたい。
さらに、参考記事。
もうちょっと現実的な値で計算
普通は3dBも減衰があるような同軸ケーブルは使わないだろう。そこで、もうちょっと現実的な数値で考えてみる。アマチュアバンドを考慮した同軸ケーブルの損失はJARLのサイトに資料がある。
これによれば、5D-2Vを20mほど引っ張れば30MHzで0.88dB、145MHzなら10mで1.05dB、5D-FBでも430MHzなら10mで1.31dBとのこと。これを元に、分かりやすいところで1dBで考えてみる。
また、アンテナは上手くマッチングが取れていない状態を考える(マッチングが取れていれば反射は起こさないので、同軸ケーブルの損失があろうがなかろうが反射波はない。つまり、SWRは1)。例えばとして、アンテナのインピーダンスが75Ωの場合で考える(伝送路は50Ω)。SWRはインピーダンスの比から75/50=1.5。
$$電圧反射係数 \ \Gamma = \frac{75-50}{75+50} = 0.2$$
反射係数からもVSWRを計算してみる。
$$電圧定在波比 \ VSWR = \frac{1 + |\Gamma|}{1 – |\Gamma|} = \frac{1 + 0.2}{1 – 0.2} = 1.5$$
電力反射係数は電圧反射係数の二乗。
$$電力反射係数 \ \Gamma_p = \Gamma ^ 2 = 0.2^2= 0.04$$
-1dBの真値は0.79なので、10Wを入力するとアンテナに7.9W届き、電力反射係数の0.04を乗じた0.316Wが反射する。さらに、戻りにも1dBのロス(0.79倍)があるので、0.24964Wが戻ってくる。これを上の式に入れる。
$$P_f = 10 \ W$$
$$P_r = P_f \times 0.79 \times 0.04 \times 0.79 = 0.24964 \ W$$
$$\frac{1+\sqrt{\frac{P_r}{P_f}}}{1-\sqrt{\frac{P_r}{P_f}}} = \frac{1+\sqrt{\frac{0.24964}{10}}}{1-\sqrt{\frac{0.24964}{10}}} = 1.375$$
アンテナのVSWRが1.5でも同軸ケーブル(やコネクタなどの合計)のロスが1dBあると、手元で見たVSWRは1.375。わずかと言えばわずかだけど、実際の値よりもよく見える。
別解として、リターンロスを使って計算してみる。
$$リターンロス \ RL = 20 log \frac{VSWR + 1}{VSWR – 1} = 13.98 \ dB$$
一応、逆算。
$$VSWR = \frac{1 + 10^{-(RL / 20)}}{1 – 10^{-(RL / 20)}} = \frac{1 + 10^{-(13.98 / 20)}}{1 – 10^{-(13.98 / 20)}} = 1.50$$
同軸ケーブルによる往復のロス(2dB)を考慮するとVSWR は、
$$\frac{1 + 10^{-((13.98 + 2) / 20)}}{1 – 10^{-((13.98 + 2) / 20)}} = 1.38$$
となる(誤差は計算に使った有効数字の桁数によるもの)。
計算はこれで合ってるかな?
なお、これは最初の前提の通り、ロス(減衰)にだけ注目して検討したもの。波長との関係でインピーダンスが違って見える(影響を受ける)のはまた別の話。




コメント
違う方向からのアプローチです
PAI型ATTで出力端をオープンにする もしくは T型ATTで出力端をオープンにすると入力端から見たインピーダンスはほぼ51オームになります。
50オームの入力端から見たATTのVSWRは大体1.02になります。
同軸ケーブルの長さでVSWRが変化する説(同軸ケーブルの損失を無視する条件下で)はどの説明でも納得できないので、非常に興味があります。電気的1/2波長の整数倍の長さにするとANT給電点と同じとなる説が一時はやりましたよね!
この辺りはヒントになりますか?
https://www.jh4vaj.com/archives/14727
無線屋ではありませんが、高周波電源を扱っている者です。参考にさせて頂いています。
最初のリンク(https://tokyoswan.web.fc2.com/4htm/swr/swr.htm)の図5は間違ってると思うんですよね(向こうのサイトで指摘したいのですが、コメント欄も無く…)。
送信機も同軸ケーブルも50Ωなら、アンテナのところで、送信機側を見ると、50Ωなだけですので。
ふたつ目のリンク(http://take103.blog.fc2.com/blog-entry-43.html)の図8.2で、上の条件の絵に任意長の50Ω同軸ケーブルの右側が50Ωと書いてあるのがソレです。
Sパラ解析ができるシミュレータを使えば一発で分かります。
損失で良く見えてしまうのは仰る通りだと思います。ケーブル損失を先に知っておかないと、とんでもないことになりますね(まぁ、大きくても1dBくらいなもんでしょうけど)。
先ほどコメントした者です。SWR計の右側の同軸ケーブルが整合器になりますね。理解できていませんでした。お騒がせしました。すみません。
すみません。確認です。先程のコメントも承認・掲載したほうが良いですか?それとも、削除しますか?
お恥ずかしいです。2月のエントリ、https://www.jh4vaj.com/archives/16219
の100Ω終端の状態と勘違いしていました。
コメントは、削除頂けるとありがたいです。よろしくお願いします。
自己レスです。再度考えましたが、
(損失が無ければ)測定位置でインピーダンスは変わるが、SWRは変わらない、ですね。
2月のエントリ、https://www.jh4vaj.com/archives/16219 の100Ω終端の場合で、等SWR円上の軌跡が描かれているのは、同じ意味(インピーダンスは変化、SWRは一定)でした。
なので、先のページの図5は、SWRが変わると表現してるのは、やはり誤りかと。
コメント欄汚してしまってすみません。
すみません。ちょっと理解が追いつけていないですけど、このブログ訪問者さんにも一連の話が分かるように、最初のコメントも公開しておきました。
自分の理解のためにも、シミュレータを動かしてみました。
添付画像に、6種類の結果があり、上から、
1.50Ω負荷
2.100Ω負荷
3.50Ω負荷を45Ωケーブルで接続
4.100Ω負荷を45Ωケーブルで接続
5.50Ω負荷を50Ωから少しずれた損失付きのケーブルで接続
6.100Ω負荷を50Ωから少しずれた損失付きのケーブルで接続
です。
グラフの青がSWR、赤とピンクが電源側から見たインピーダンスの実部と虚部です。
2は、https://tokyoswan.web.fc2.com/4htm/swr/swr.htm の図5の状態で、SWRは2で一定ですが、電源側から見たインピーダンスは、周期的に変化しています。
3と4から、ケーブルの特性インピーダンスが50Ωからずれていると、SWRが周期的に変化することが分かります。
損失有りの5と6は、https://www.jh4vaj.com/archives/16219 の結果とほぼ同じものではないかと思います。