SWRと電力の関係
SWRの計算で「進行波電力」と「反射波電力」という言葉が出てくる。単純なイメージでは、進行波電力が送信機が送り出した電力、反射波電力がアンテナから戻ってきた電力という気がする。しかし、そんな単純なものではないようだ。
SWR=1で反射がない場合は、送信電力と進行波電力は一致する(はず)。しかし、SWR≠1で反射が生じると両者は一致しない。進行波電力は言わば「見かけ上の電力」。反射波電力も同様。詳細はこちらの記事。
こちらの記事から図を一つ引用。
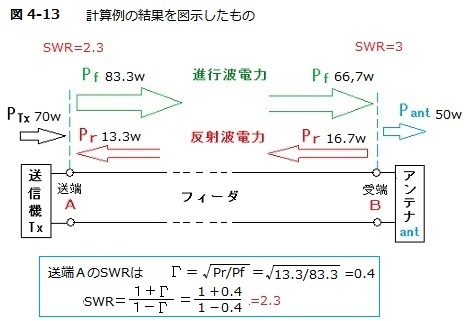
この図は、マッチングが取れていない場合の例。前提条件として、フィーダ(同軸ケーブル)のロスは1dB。
- 送信機から70Wの電力を送ると送信機端での進行波電力は83.3W(送信電力よりも大きくなる)
- アンテナのSWRを元に計算するとこうなるらしい(ややこしいので詳細は元記事を参照)
- 一応、式にするとこう(SはSWR(=3))
- \(アンテナ端P_f=P_{ant}\frac{(S+1)^2}{4S}=50\frac{(3+1)^2}{4\times 3}=\frac{800}{12}=66.7W\)
- 1dB(ケーブルロス)は真数で約0.8なので送信機端でのPfは次のとおり
- \(66.7/0.8=83.3W\)
- アンテナ端での進行波電力は66.7W、反射波電力は16.7W
- \(アンテナ端P_r=P_{ant}\frac{(S-1)^2}{4S}=50\frac{(3-1)^2}{4\times 3}=\frac{200}{12}=16.7W\)
- アンテナに送られる電力は差引き50W
- \(SWR=\frac{1+\sqrt{16.7/66.7}}{1-\sqrt{16.7/66.7}}=3.0\)
- アンテナのSWRが3であることが前提の話なので当然だけど
- 送信機端での反射波電力は13.3W(同軸ケーブルによるロスのため)
- \(送信機端P_r=16.7\times 0.8=13.3W\)
- \(83.3-13.3=70\)、これが送信機の出力電力
- \(SWR=\frac{1+\sqrt{13.3/83.3}}{1-\sqrt{13.3/83.3}}=2.3\)
アンテナのSWRが3の場合、70Wで送信して20W(約29%)がロス(同軸ケーブルで熱)になり、アンテナに送り込まれるのは50W。しかも、送信機端でのSWR(見かけ上のSWR)は2.3。
送信機の側にSWR計をつないで反射波電力を読んで「13Wか。ということはアンテナには70-13=57W行ってる」というのは正しくない。これについてはこちらの記事でさらに詳しく解説されている。
一連の記事、とてもためになる。
まぁ、難しいことはさておき、アンテナのSWRを下げることと、同軸ケーブルのロスを抑えること(損失の小さなケーブルで、かつ、できるだけ短く)が重要ってことは間違いない。
計算例
さて、ここまではSWRが3という極端とも言える場合の話。SWRがこんな状態で使う人はあまりいないはず。では、もうちょっと現実的なところでSWRが2や1.5だったらどうか?上の式を使って計算してみる。
SWR=2の場合
上の計算例に合せるため、アンテナに供給される電力を50W、ケーブルロスを1dB(0.8)とする。
- アンテナ端
- \(アンテナ端P_f=P_{ant}\frac{(S+1)^2}{4S}=50\frac{(2+1)^2}{4\times 2}=\frac{450}{8}=56.3W\)
- \(アンテナ端P_r=P_{ant}\frac{(S-1)^2}{4S}=50\frac{(2-1)^2}{4\times 2}=\frac{50}{8}=6.3W\)
- 念のため検算: \(SWR=\frac{1+\sqrt{6.3/56.3}}{1-\sqrt{6.3/56.3}}=2.0\)
- 送信機端
- \(送信機端P_f=アンテナ端P_f/0.8=56.3/0.8=70.4W\)
- \(送信機端P_r=6.3\times 0.8=5.0W\)
- \(送信機出力=70.4-5.0=65.4W\)
- \(SWR=\frac{1+\sqrt{5.0/70.4}}{1-\sqrt{5.0/70.4}}=1.7\)
まとめると、送信機から65.4Wを出力してアンテナに50W行くので、15.4W(24%)の損失。送信機端で見たSWRは1.7。
SWR=1.5の場合
同様に、アンテナに供給される電力を50W、ケーブルロスを1dB(0.8)とする。
- アンテナ端
- \(アンテナ端P_f=P_{ant}\frac{(S+1)^2}{4S}=50\frac{(1.5+1)^2}{4\times 1.5}=52.1W\)
- \(アンテナ端P_r=P_{ant}\frac{(S-1)^2}{4S}=50\frac{(1.5-1)^2}{4\times 1.5}=2.1W\)
- 念のため検算: \(SWR=\frac{1+\sqrt{2.1/52.1}}{1-\sqrt{2.1/52.1}}=1.5\)
- 送信機端
- \(送信機端P_f=アンテナ端P_f/0.8=52.1/0.8=65.1W\)
- \(送信機端P_r=2.1\times 0.8=1.7W\)
- \(送信機出力=65.1-1.7=63.4W\)
- \(SWR=\frac{1+\sqrt{1.7/65.1}}{1-\sqrt{1.7/65.1}}=1.4\)
まとめると、送信機から63.4Wを出力してアンテナに50W行くので、13.4W(21%)の損失。送信機端で見たSWRは1.4。
「21%の損失」というと大きいように思うが、そもそも同軸ケーブルによるロスが1dBという想定なので、これだけで20%が失われる。つまり、SWRが1.5であることによる損失の増加分は1%ほどという計算になる。合ってる?
ケーブル損失が0.5dBの場合
元記事の「ケーブル損失1dB」というのは、21MHzで5D-2Vを20mという想定。同軸ケーブルの仕様書を見ると、30MHzで46dB/km、10MHzで26dB/kmの損失らしい。そうすると、7MHzで20mなら約0.5dB程度か?
ということで、0.5dBのケーブル損失、アンテナSWRが2の場合も計算してみる。0.5dBの損失ということは真数では約0.9。
- アンテナ端
- \(アンテナ端P_f=P_{ant}\frac{(S+1)^2}{4S}=50\frac{(2+1)^2}{4\times 2}=56.3W\)
- \(アンテナ端P_r=P_{ant}\frac{(S-1)^2}{4S}=50\frac{(2-1)^2}{4\times 2}=6.3W\)
- 念のため検算: \(SWR=\frac{1+\sqrt{6.3/56.3}}{1-\sqrt{6.3/56.3}}=2.0\)
- 送信機端
- \(送信機端P_f=アンテナ端P_f/0.9=56.3/0.9=62.6W\)
- \(送信機端P_r=6.3\times 0.9=5.7W\)
- \(送信機出力=62.6-5.7=56.9W\)
- \(SWR=\frac{1+\sqrt{5.7/62.6}}{1-\sqrt{5.7/62.6}}=1.9\)
まとめると、送信機から56.9Wを出力してアンテナに50W行くので、6.9W(12%)の損失。送信機端で見たSWRは1.9。
ここのまとめ
同軸ケーブルのロスが1dBでアンテナのSWRが2だと、アンテナに送り込める電力は送信出力の76%(24%損失)。一方、ケーブルロスが0.5dBの場合は同じくアンテナSWRが2でも、アンテナに送り込める電力は88%(12%損失)。
| 条件 | SWR 3 同軸損失 1dB | SWR 2 同軸損失 1dB | SWR 1.5 同軸損失 1dB | SWR 2 同軸損失 0.5dB |
|---|---|---|---|---|
| 効率 | 71% | 76% | 79% | 88% |
| 損失 | 29% | 24% | 21% | 12% |
| 送信機端で見たSWR | 2.3 | 1.7 | 1.4 | 1.9 |
こうして並べてみると、SWRが1.5だとか2だとかよりも、同軸ケーブルによる損失の方が遥かに影響大。アンテナのSWRが1.5なら本当に充分で、それをもっと下げようとするよりも、「損失の小さい同軸を使え」ってことか。SWRが2でも同軸ケーブルの損失が小さければ問題なさそうだとも思う。まぁ、SWRは1に近いほど気持ちはいいけど。
例えば、430MHzだと8D-2Vでも損失は10m辺り1.35dBらしい。かなり大きいと言えそう。ここでさらにMコネなんか使った日にゃ…。VHF/UHFは大変だ。
ちなみに、RG-58C/Uの損失は10mあたり、10MHzで約0.5dB、30MHzで約0.8dB。詳しくはこちらの記事。



コメント
面白い記事をありがとうございます。
数式はまだ理解できないですが、感覚的にもその通りと感じてます。
swr2とswr1で飛びが変わらないと思うので。
一つ疑問だったのですが、アンテナ直下でアンテナチューナーを使った場合はどうなるのでしょうか?
反射波がゼロになるだけで、アンテナへの供給電力は変わらない?のでしょうか。
「多分こうじゃないかと思う」という話です。
ATUの両側どちらもマッチングが取れているように見える状態ですよね。そうであれば、
という状況になると思います。であれば、同軸とATUによるロス分以外はすべてアンテナに供給されるのではないでしょうか?
補足です。
上の表で同軸の損失が1dBの場合、効率はSWR 2では76%、SWR 1.5では79%であり、3%分の違いです。
単純に損失が1dBの場合(反射を考えない場合=SWR 1.0)は、効率は79%です。SWR 1.5の場合と変りませんね。桁数を増やすと違いが見えますが(SWR 1.5では78.9%、SWR 1.0では79.4%)。
一般的にSWR 1.5程度なら問題無しとしていると思いますが、それはこの計算からわかりますね。
また、SWR 2.0程度であれば、ATUを入れるとそれによるロスのほうが大きそうです。
・送信機から70Wの電力を送ると送信機端での進行波電力は83.3W(送信電力よりも大きくなる)
これはエネルギー不変の法則に反します。
送信機端での反射電圧と反射電流(つまり反射電力)は、送信機内で消費されると考えられます。
詳しい説明はリンク先にあります。
「(送信電力よりも大きくなる)」というのは理屈に合いませんね。本当だとすると無から有へのエネルギー発生装置になります。
反射波を考慮する必要があります。
もう一度書いておきます。詳細はリンク先をご覧ください。念のためURLをここにも書いておきます。
http://take103.blog.fc2.com/blog-entry-37.html