こないだPWMのデューティ比を変える実験をやったので、今回はその応用編。正弦波を出力してみる。なお、ここのでのArduinoは「Arduino UNO(互換機)」のこと。
プログラム
やることは簡単。一定のタイミング(割込み)で正弦波に応じたアナログ値(PWMのデューティ比を変える)を出力するだけ。
#include <avr/io.h>
#define PIN_SIN_WAVE 9 /* 正弦波出力ピン */
#define N_WAVE 32 /* 正弦波テーブルの数 */
unsigned int wave[N_WAVE]; // 正弦波テーブル
volatile int i_wave; // 正弦波テーブルの参照ポインタ
void setup() {
float unit_deg;
int i;
i_wave = 0;
/* 正弦波テーブル作成 */
unit_deg = (2.0 * 3.141592) / (float)(N_WAVE);
for (i = 0; i < N_WAVE; i++) {
wave[i] = (unsigned int)((((sin(unit_deg * (float)i) + 1.0) / 2.0) * 255.0) + 0.5);
}
/* 正弦波出力割込み周期設定 */
TCCR2A = 0x02; // WGM2 = 0x2(CTC), CS2 = 0x1
TCCR2B = 0x02;
OCR2A = 63; // 割込タイミング
TIMSK2 = 0x02; // TC2比較割込みA許可
/* 正弦波用PWM周波数設定 */
pinMode(PIN_SIN_WAVE, OUTPUT); // pin 9 -> OC1A
TCCR1A = 0x81; // COM1A = 0x2, WGM1 = 0x5
TCCR1B = 0x09; // CS1 = 0x1
analogWrite(PIN_SIN_WAVE, 127);
}
/* 割込み: 正弦波出力 */
ISR (TIMER2_COMPA_vect) {
if (i_wave >= N_WAVE) {
i_wave = 0;
}
analogWrite(PIN_SIN_WAVE, wave[i_wave]);
i_wave++;
}
void loop() {
}以下、処理をざっくりと説明。
正弦波テーブル作成
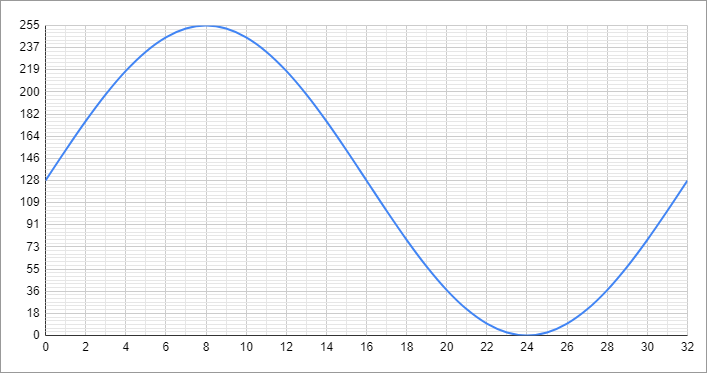
正弦波出力を得るには、その正弦波を時間軸(横軸)でぶつ切りにして、そのタイミングに応じたレベル(縦軸)を出力すればよい。出力のときにいちいち計算するのは計算時間コストが高いので、予めテーブル(表)にして持っておく。1周期だけ持っておけばあとは繰り返しで使える(最小限にするなら1/4周期分だけ持っておいて、あとはそれを反転させたりして使うこともできるが、それも面倒なので、ここでは素直に1周期分の表を作る)。
時間軸での分割数は、サンプリング定理によれば信号の周波数の二倍以上で標本化すれば良い。とは言え、あまりにもサンプリング数が少ないと信号波形のピークが拾えない。極端な場合を考えると、ぴったり二倍の周期でサンプリングした場合、最初のポイントが0だった場合、次のポイントはちょうど半周期なのでまた0、その次はぴったり1周期でまた0、以降、ずっと0のレベルばかりを拾ってしまう(上の図で言えば、縦軸128のポイントばかりを取ることになる)。
ここでは、とりあえず32に分割してみる(N_WAVE)。
出力にはArduinoのanalogWrite()を使うので、指定できる範囲は範囲は0~255。sin()の引数は角度(ラジアン)で、その戻り値は-1~+1。これらを踏まえると、正弦波のテーブルを作る計算式は次のようになる。
unit_deg = (2.0 * 3.141592) / (float)(N_WAVE);
for (i = 0; i < N_WAVE; i++) {
wave[i] = (unsigned int)((((sin(unit_deg * (float)i) + 1.0) / 2.0) * 255.0) + 0.5);
}sin()の戻り値が-1~+1なので、1の下駄を履かして0~2にし、それ2で割って0~1に。さらに255を掛けて0~255。最後の+0.5は整数に丸める際の四捨五入。
正弦波出力割込み周期設定
作成した正弦波テーブルを一定のタイミングで読み出してanalogWrite()で出力するのだけど、その「一定のタイミング」はタイマ割込みで実現する。使用するタイマはTC2(特別な理由があるわけでもないので他でもよい)。
出力する正弦波を1kHzとすると、1周期を32分割して出力するので、割込みのタイミングは32kHz。Arduinoのクロックは16MHzなので、32kHzは500クロック分。TC2は8ビットカウンタなので500は数えられない。そのため、タイマ用のロックはシステムクロックを8分周して使用する。500/8=62.5なので、63クロックごとの割込みで約1kHzになる。
- CTC動作
- OCR2Aと一致で割込み
- 比較割込みAを使用
- クロック分周: 8
TCCR2A = 0x02; // WGM2 = 0x2(CTC), CS2 = 0x1
TCCR2B = 0x02;
OCR2A = 63; // 割込タイミング
TIMSK2 = 0x02; // TC2比較割込みA許可正弦波用PWM周波数設定
ArduinoのPWMの周波数は標準では490Hz、または、980Hz(ピンによる)。作りたいのが1kHzなので、その元となるPWMの周波数が490Hzとかでは話にならない。また、analogWrite()でのPWM出力をLPFに通した(アナログ値化した)際のリプルを小さく抑えたいのでPWM周波数は高いほうが有利。そこで、デューティ比が256階調確保できる最大周波数の62.5kHzとする。このあたりの詳細はこちらの記事。
出力ピンは9を使うことにするので、関連するレジスタ設定はこうなる。
pinMode(PIN_SIN_WAVE, OUTPUT); // pin 9 -> OC1A
TCCR1A = 0x81; // COM1A = 0x2, WGM1 = 0x5
TCCR1B = 0x09; // CS1 = 0x1
analogWrite(PIN_SIN_WAVE, 127);最後の行のanalogWrite()は出力の初期値。なくてもかまわないけど、一応。
割込み: 正弦波出力
割込周期の設定のところで説明したように、TC2での比較一致Aを使う。そのため、指定するベクタはTIMER2_COMPA_vect。
割込処理の内容は、予め用意した正弦波テーブルから読み出してanalogWrite()するだけ。テーブルのポインタがi_wave。読み出すたびにインクリメントし、テーブルの上限まで行ったら頭に戻る。
ISR (TIMER2_COMPA_vect) {
if (i_wave >= N_WAVE) {
i_wave = 0;
}
analogWrite(PIN_SIN_WAVE, wave[i_wave]);
i_wave++;
}正弦波出力観測
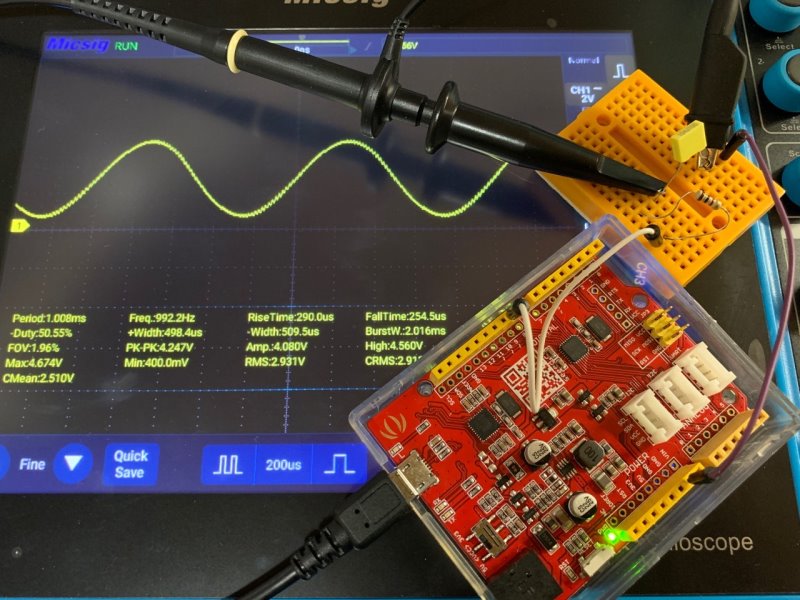
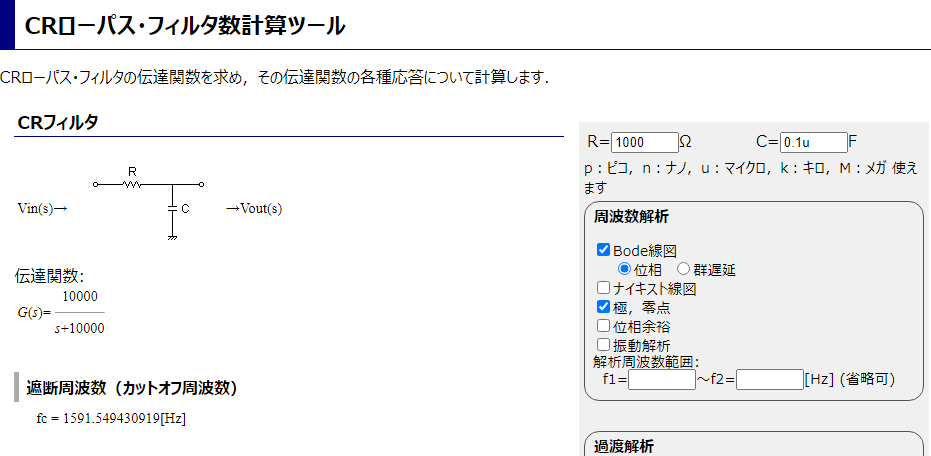
では、実際にArduinoを使って出力させてオシロスコープで見てみる。出力はCRによるローパスフィルタを通す。1000Ω、0.1μFで、計算上のカットオフ周波数は約1.6kHz。計算にはこちらのツールを使わせてもらった。
割込タイミング変更による周波数の変化
出力周波数は1kHzで設計したが、割込タイミング(OCR2A設定値)を変更すれば他の周波数にもできる。ということで、いくつか観測する。
OCR2A: 255(244Hz)
255はOCR2Aの最大値。
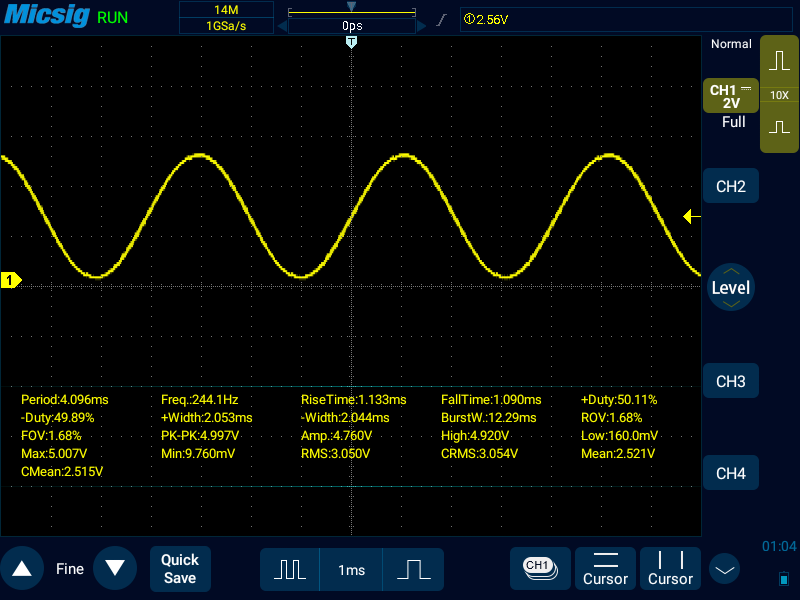
OCR2A: 127(488Hz)
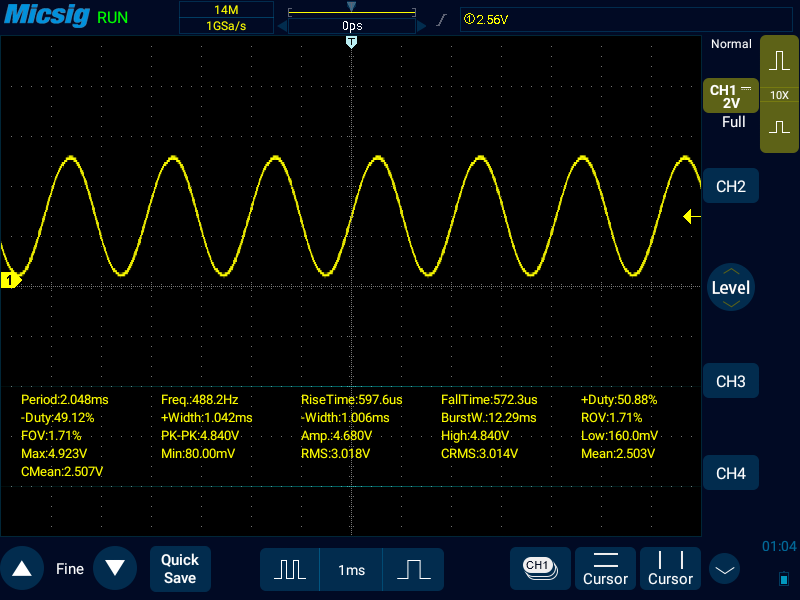
OCR2A: 63(976Hz)
これが設計値の1kHz。誤差は約2.4%。本来ならOCR2Aに設定すべき値は62.5なのだけど、整数しか取れないので63。そのためやや遅め(周波数が下がる)。
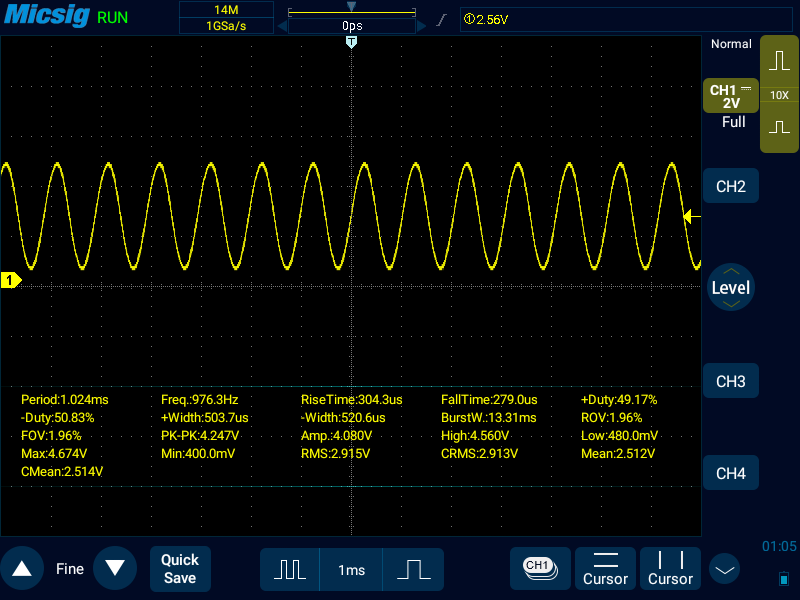
ちなみに、カウンタを62にしたものが下の図で、991Hz(横軸のスケールが違うことに注意)。
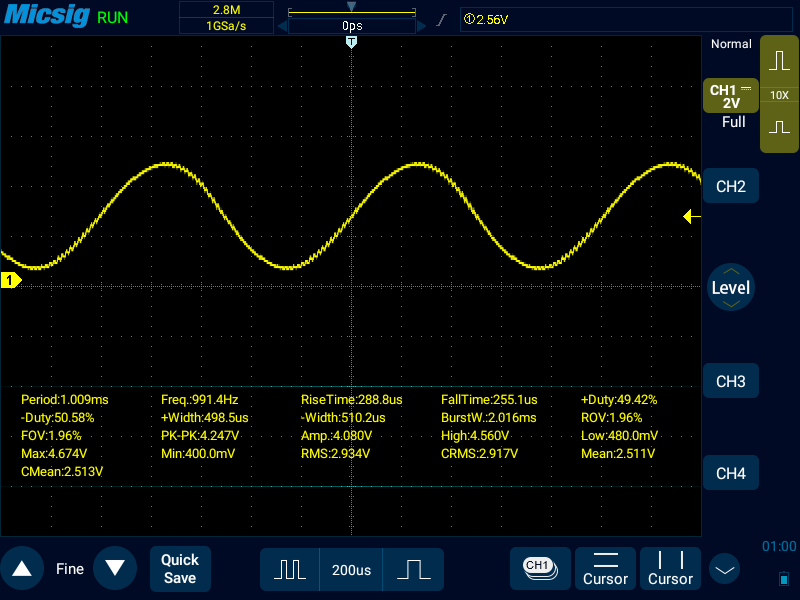
OCR2A: 31(1951Hz)
LPFのカットオフ周波数を超えるので、正弦波の振幅が小さくなってくる。
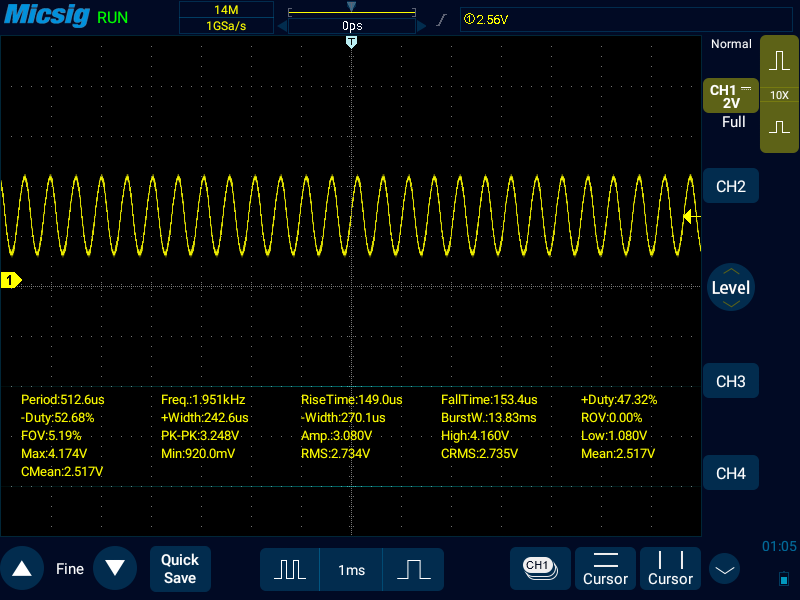
OCR2A: 15(2617Hz)
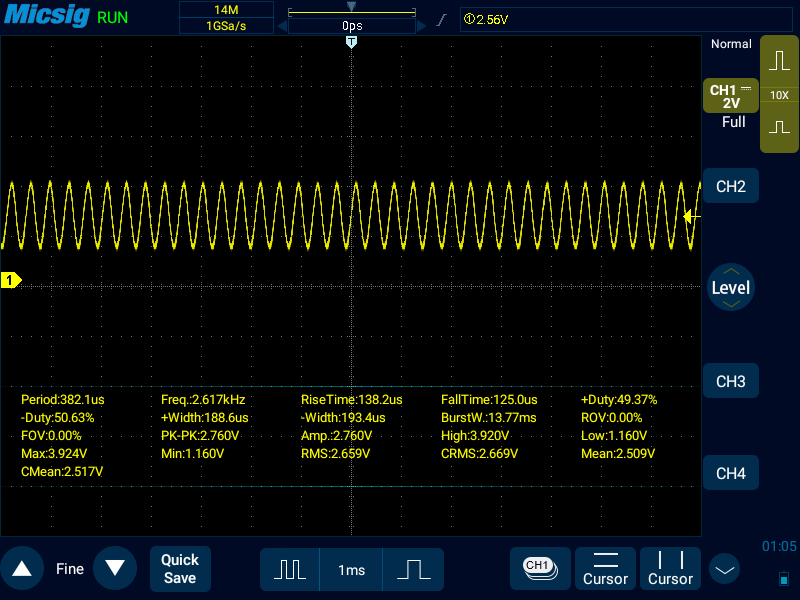
OCR2Aの設定値を半分にするごとに出力周波数は2倍になっていたが、ここでは2倍にならずに2600Hzくらいで頭打ちになっている。このあたりが割込処理の所要時間による上限か?大雑把な感覚として、頭打ちの時間がOCR2Aが25だとすると、システムクロックはその8倍の200クロック。これだけの時間しかないのだからしょうがないか。
リプル
出力波形をよく見ると、PWMの周波数によるリプルが見える。
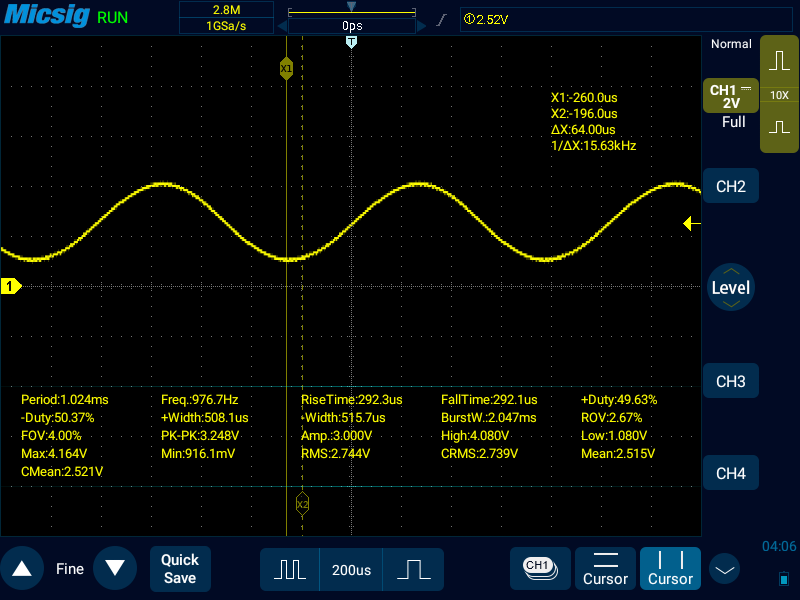
拡大すると、周期が想定通り62.5kHzだということもよく分かる。
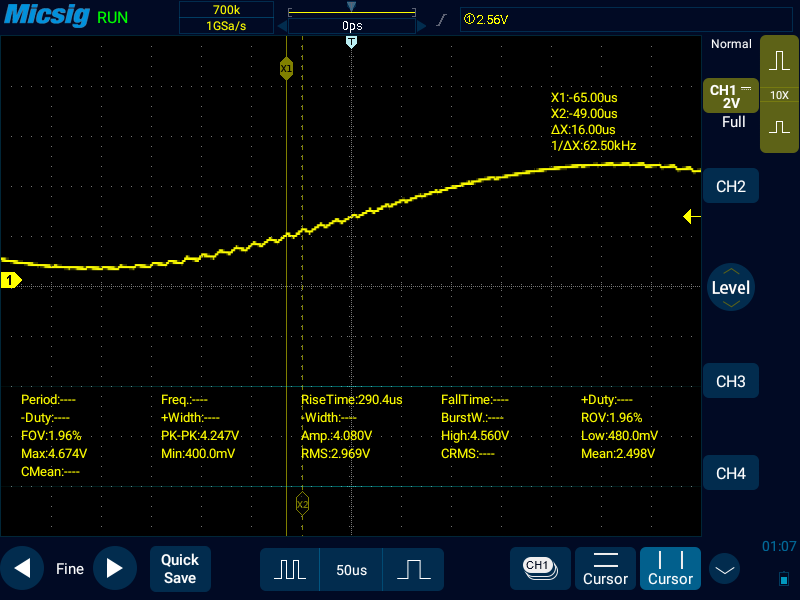
こうやって拡大すると気になってしまうので、LPFをもう1段入れてみる。先にカットオフ周波数約34kHz(47Ω、0.1μF)のLPFを入れてPWMによるリプル対策をし、その後に約1.6kHz(1000Ω、0.1μF)のLPFで正弦波を通す。
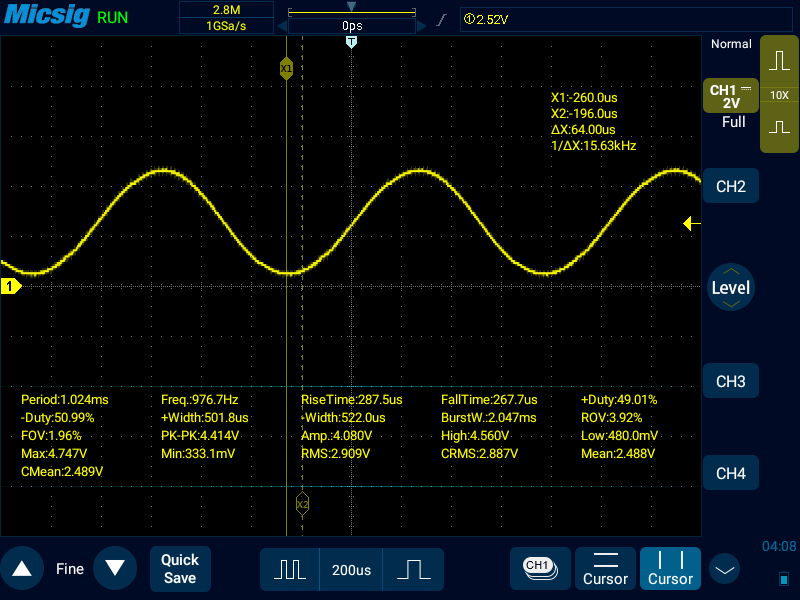
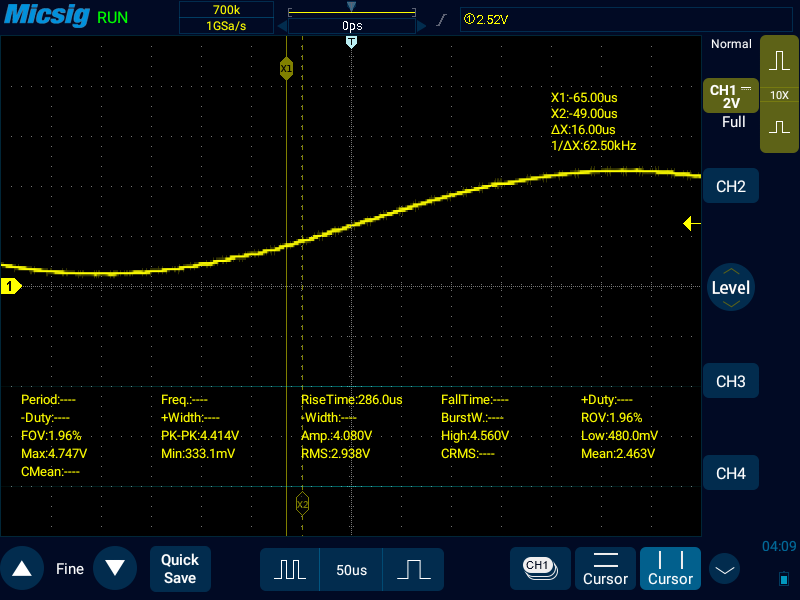
だいぶ滑らかになった。なお、LPFの順序を逆にしても同様にPWMのリプルは小さくできるが、正弦波の振幅も小さくなる。
サンプリング数
ここまで1周期を32分割したもので波形を生成した。では、今度は、サンプリング数を減らすとどうなるかの実験。正弦波テーブルの数を減らし、それに応じて割込タイミングを早めれば同じ周波数の出力が得られるはず。
LPFの1段目(PWMリプル処理)と、2段目(最終出力)の両方を見てみる。青が1段目、黄が2段目。
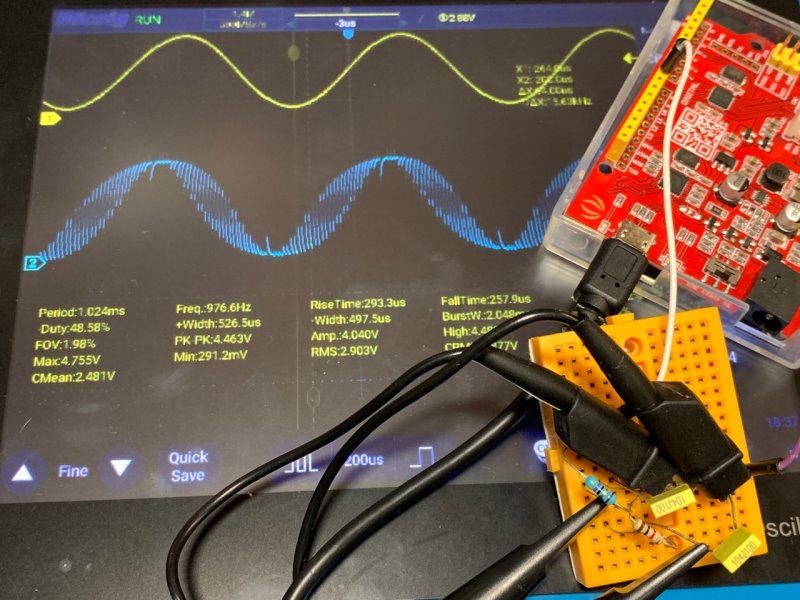
サンプリング数: 32(OCR2A: 63)
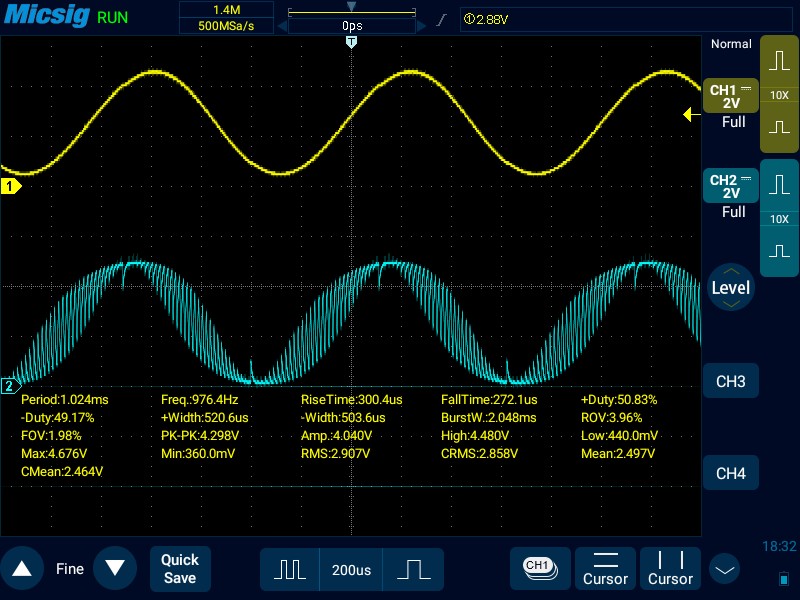
サンプリング数: 16(OCR2A: 31)
1周期中に16の階段状が見て取れる。
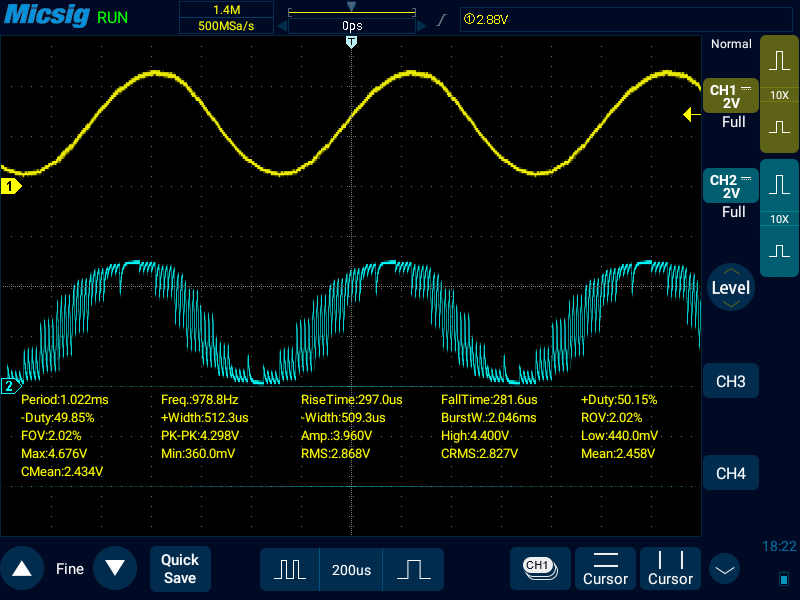
サンプリング数: 8(OCR2A: 15)
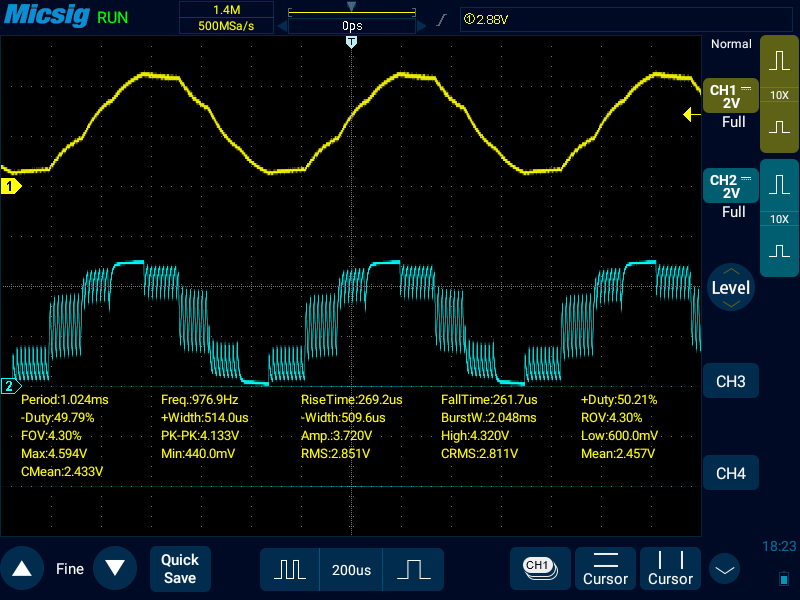
OCR2Aが15ということは、割込処理が間に合っていない可能性。これ以下は確実に間に合っていないので測定しても意味がない。
おまけ: サンプリング数32のときの拡大波形
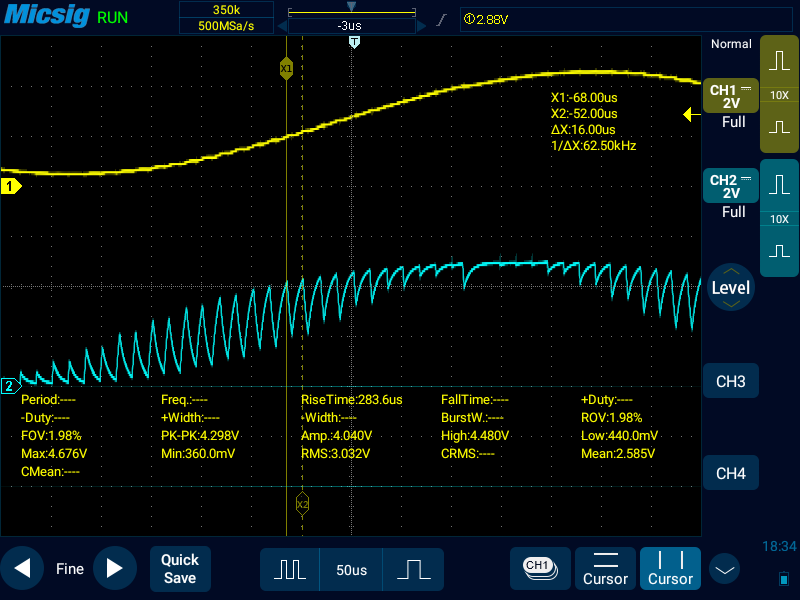
以上、1kHz程度の正弦波であれば、結構きれいなものを出せそう。




コメント