先日、AliExpressで買った抵抗を測ったところ、仕様(誤差±1%)を満たしていなかったという記事を書いた。
今度は、比較として、秋月電子通商で購入したものを測ってみる。仕様は同じく、金属皮膜抵抗 100Ω 1% 1/4W。ただし、外形は小型のもの。
袋から無作為に10本取り出して測定。

測定結果: 99.72, 99.79, 99.63, 99.97, 100.12, 100.13, 99.98, 100.20, 99.42, 99.60
ちゃんと±1%の範囲に収まっている。すごい、じゃなくて、これが当り前でしょ?
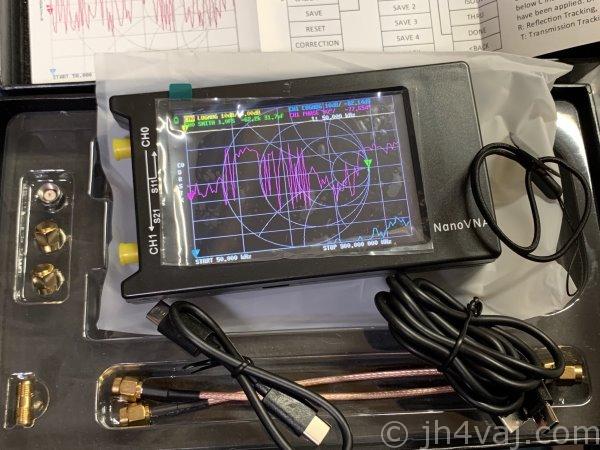
ちなみに、測定に使ったのはDE-5000という高精度LCRメータ。これも秋月電子で購入したもの。





コメント
秋月とAliの平均値、3σをExcelで計算しました。
秋月
平均値:99.856
3σ:0.788060911
6σ:1.576121823
よって、99.06794~100.6441の間に99.6%が入ります。
これを±1%と言って売るには気が引けます。なぜなら6σが1.576121823もあるからです。
日本メーカーの受け入れ検査ではNGになるような気がします。
Ali
平均値:98.86
3σ:4.6904584
よって、94.1695416~103.5504584の間に99.6%が入ります。
これ、±5%でも売れないレベルです。
コメントありがとうございます。そう言うものなんですね。まったく知らない世界です。
日本メーカの受入基準だと、1%は(一般的に)どの範囲なんでしょうか?
専門にやっていた訳ではなくて、歩留まりの話を聞いていたレベルの素人ですが、
製品を作る上で製品の規格内に収まる確率を表す、工程能力Cp/Cpkというものがあります。
詳しくは統計や生産管理の本に譲りますが、不良率として
の関係があります。
秋月のCp値は1.27ですので、日本メーカーの一般的な値1.5(4.5σ)には届きません。
Aliの場合は±5%でも、Cp値が1.07でとても使えないレベルです。
ただし、サンプルが10本と少ないので、あくまで参考です。データとして意味を持たせるにはサンプルが100本程度は必要だと思います。
参考にはこちらのサイトなどがあります。
ばらつきと工程能力
http://www.placeon.jp/blog/words/words_monozukuri/process_ca…
日本メーカーの目標は6σです。10億個で不良が2個ですね。
ありがとうございます。とてつもなく厳しいということがわかりました^^;
仮に、製品を構成する部品が1,000点あるとしたら、不良確率は1,000になるでしょうから、100万台で2台の不良ということでしょうか。
設計者が余裕を持った設計をすれば、個々の部品が規格から多少外れていたとしても問題なくでしょう。と考えると、動作に問題が生じる可能性はほぼないでしょうね。しかし、メーカとしてはそのくらいじゃないと、修理等の対応が大変になるんでしょうね。
それから、あれではサンプル数が少ないことは理解しています。ですが、今回の場合は100本測定したら抜き取りチェックではなくて、全数チェックになります。余談ですけど。
なお、勝手ながら、表などの体裁をこちらで整えさせてもらいました。ご了承ください。
ちょっと乱暴な計算をしてみます。
仮に4.5σ 不良率3.4PPMの部品1,000個で作られる製品があったとして
部品1個の良品の確率は1-3.4PPM = 0.9999966です。
1,000個なので出来上がりの良品の確率は個々の部品の良品の確率の掛け算になって、
0.9999966^1,000=0.996605768です。
つまり製品の良品の確率は99.7%です。約0.3%の不良が出る事になります。
実際はバラつきを考慮した設計や検査・調整工程などがあるでしょうから、そう悪くならないのでしょうけど。
ちょっと視点が異なっていました。
それぞれが販売する抵抗の公称精度(±1%)と実力値の確認と思ってしまいました。
ありがとうございます。前の私のコメントはあまり深い意味はありません。漠然と、不良品率を下げるためには個々の部品の精度が非常に重要なんだなぁ、という感想みたいなものです。